| Аббревиатура | Расшифровка | Значение |
| ATA | Actual Time of Arrival | Фактическое время прибытия транспортного средства |
| ATD | Actual Time of Departure | Фактическое время отплытия (вылета, выезда) |
| AWB | Air Waybill | Авианакладная, сопровождающая груз. Может быть двух видов:
|
| BAF | Bunker Adjustment Factor | Дополнительный топливный сбор. Взимается как часть от суммы фрахта или как фиксированная сумма за 1 TEU. |
| B/L | Bill of Lading | Коносамент, документ, сопровождающий товар. Используется при морских перевозках и мультимодальных перевозках с использованием морского транспорта. Используется при морских перевозках и мультимодальных перевозках с использованием морского транспорта. |
| CAF | Currency Adjustment Factor | Дополнительный сбор, взимается как надбавка или часть от суммы фрахта, зависит от колебаний курса валют. |
| CFS | Container Freight Station | Контейнерный пункт |
| CMR | Convention relative au Contrat de transport international de merchandises par route | Международная товаротранспортная накладная для автомобильных перевозок |
| CNEE | Consignee | Грузополучатель |
| CNOR | Consignor | Грузоотправитель |
| C/O | Certificate of Origin | Сертификат происхождения. Используется для определения страны происхождения (производства) товара. |
| COC | Сarrier’s Оwned Container | Контейнер в собственности перевозчика. Стоимость его использования включена во фрахт. |
| CSC | Carrier security charge | Плата за обеспечение безопасности перевозчика. |
| C.S.C | Container Service Charge | Плата за передачу поставок от причала перевозчику и наоборот. |
| CY | Container Yard | Контейнерный терминал |
| DIM | Dimensions | Размеры груза |
| DGR | Dangerous Goods Regulations | Правила перевозки опасных грузов |
| DOC | Documentation fee | Плата за оформление документов |
| DTHC | Destination terminal handling charges | Погрузо-разгрузочные работы в порту назначения |
| ETA | Estimated Time of Arrival | Ожидаемое время прибытия товара на место назначения |
| ETD | Estimated Time of Departure | |
| EX-1 | Export declaration | Экспортная декларация. Документ, предоставляющий все сведения об экспортируемых товарах. Документ, предоставляющий все сведения об экспортируемых товарах. |
| FCL | Full Container Load | Полная загрузка контейнера |
| FEU | Forty foot equivalent Unit | 40-футовый контейнер |
| FIATA | Federation International des Associations de Transitaires et Assimiles | Международная ассоциация экспедиторов |
| FI/FO | Free in/Free out | Без погрузки/выгрузки товара в порту |
| FIO | Free in and out | Судно не платит за погрузку и выгрузку. |
| FIOS | Free in and out and stowed | Судно не платит за погрузку, выгрузку и укладку товара на борту. |
| FT | Flat Rack | Контейнер-платформа с торцевыми стенками |
| HBL | House B/L | Коносамент, выданный экспедитором (домашний) |
| HQ | High Cube | 40-футовый контейнер High Cube. Обладает большей вместимостью по сравнению с обычным контейнером. |
| IATA | International Air Transport Association | Международная ассоциация воздушного транспорта |
| IG | In Gauge | При доставке груза при помощи спецтехники – размеры груза не превышают размеров платформы. |
| INV | Commercial Invoice | Инвойсный счет – выписывается продавцом, используется для указания ценности товара. |
| L/C | Letter of Credit | Аккредитив. Подписывается в момент заключения контракта. Определяет условия платежа и сроки доставки товара. |
| LCL | Less than Container Load | Консолидированная перевозка – несколько грузов объединяются в одном контейнере. |
| LI/LO | Liner in/out | Погрузка и выгрузка товара за счет линии |
| LO/LO | Lift on/Lift off | Груз поднимается и опускается |
| LT | Local Time | Местное время |
| MBL | Master B/L | Основной коносамент. Выдается морской линией. Выдается морской линией. |
| MV | Mother Vessel | Крупнотоннажное линейное судно |
| N/N | Nоn-negotiable Document | Документ, который не дает права на получение товара. |
| NVOCC | Non Vessel Operating Common Carrier | Брокер, продающий место под загрузку на судах, которыми он не владеет. |
| OBL | Original B/L | Оригинал коносамента |
| OOG | Out of Gauge | При доставке груза при помощи спецтехники – размеры груза превышают размеры платформы. |
| OT | Open Top | Контейнер без жесткой крыши |
| OTHC | Original terminal handling charges | Погрузо-разгрузочные работы в порту отправки |
| ORC | Origin receiving charges | Сборы в Китае |
| PACK | Packing List | Упаковочный лист. Дает представление о месте нахождения товара в грузе. |
| PCS | Port Congestion Surcharge | Сборы, зависящие от загруженности контейнерного терминала. |
| POD | Port of Destination | Порт назначения |
| POL | Port of Loading | Порт отправления |
| PSS | Pick Season Surcharge | Надбавка к фрахту, зависящая от сезонных колебаний спроса на перевозки. |
| RO/RO | Roll-on/Roll-off | Судно, принимающее на борт накатные грузы. |
| SWB | Sea Way Bill | Морская накладная |
| TEU | Twenty foot Equivalent Unit | 20-футовый контейнер |
| THC | Terminal Handling Charge | Портовый сбор за передачу контейнера от причала перевозчику и наоборот. |
| TLC | Three-Letter-Code | Трехзначный код аэропорта |
| T/S | Transshipment | Перегрузка судна |
| T/T | Transit Time | Транзитное время перевозки |
| T-1 | Transit declaration | Транзитная таможенная декларация |
| ULD | Unit Load Device | Контейнеры, паллеты, модули для погрузки багажа на борт самолета. |
| WHS | War Risk Surcharge | Надбавка к фрахту. Учитывает риск гибели судна и потери груза от военных действий. |
Авиационные сокращения
| А/А | Air to Air | Воздух — Воздух |
| AAF | Army Air Field | Военный аэродром |
| AAL | Above Aerodrome Level | Над уровнем аэродрома |
| AAS | Airport Advisory Service | Консультативное обслуживание в аэропорту |
| АВ | Air Base | Авиабаза |
| ABM | Abeam | На траверзе |
| ABN | Aerodrome Beacon | Аэродромный маяк |
| AC | Air Carrier | Авиаперевозчик, авиакомпания |
| АСА | Arctic Control Area | Арктический диспетчерский район |
| ACAS | Airborne Collision Avoidance System = TCAS | Бортовая система предотвращения столкновений |
| ACARS | Airbone Communications Addressing and Reporting System | Бортовая система связи с адресацией и сообщением |
| ACC | Area Control Center | Районный диспетчерский центр |
| ACFT | Aircraft | Воздушное судно |
| ACH | АТС Flight Pian Change Message (IFPS) | Сообщение об изменении плана полета (IFPS) |
| ACN | Aircraft Classification Number | Классификационное число воздушного судна |
| AD | Aerodrome | Аэродром |
| ADA | Advisory Area | Консультативный район |
| ADCS | Advance Customs | Предварительное уведомление о необходимости таможенного обслуживания |
| ADEP | Aerodrome of Departure | Аэродром вылета |
| ADES | Aerodrome of Destination | Аэродром назначения |
| ADF | Automatic Direction Finding | Автоматический радиокомпас |
| ADIZ | Air Defense Identification Zone | Зона опознавания ПВО |
| ADR | Advisory Route | Консультативный маршрут |
| ADS | Automatic Dependent Surveillance | Автоматическое зависимое наблюдение |
| ADV | Advisory Area | Консультативный район |
| AEIS | Aeronautical Enroute Information Service | Обслуживание аэронавигационной информацией на маршруте |
| AER | Approach End Runway | Конец ВПП со стороны подхода |
| AERADIO | Air Radio | Радиостанция (обслуживающая полеты) |
| AERO | Aerodrome | Аэродром |
| AES | Aerodrome Emergency Services | Аэродромная аварийная служба |
| AF Aux | Air Force Auxiliary Field | Вспомогательный аэродром ВВС |
| AFB | Air Force Base | База ВВС |
| AFIL | Flight Plan Filed in the Air | Зафайленый(Переданный) с борта план полета |
| AFIS | Aerodrome Flight information Service | Аэродромная служба полетной информации |
| AFN | American Forces Network | Сеть американских ВВС |
| AFP | АТС Flight Plan Proposal Message (IFPS) | Сообщение о предлагаемом плане полета (IFPS) |
| AFRS | Armed Forces Radio Stations | Радиостанции ВВС |
| AFS | Air Force Station | Станция ВВС |
| AFS | Aeronautical fixed service | Авиационная фиксированная служба |
| AFSS | Automated Flight Service Station | Автоматическая станция полетного обслуживания |
| A/G | Air-to-Ground | «Воздух—Земля» |
| AGL | Above Ground Level | Над уровнем земли |
| AGN1S | Azimuth Guidance Nose-in-Stand | Азимутальное наведение ВС носом на стоянку |
| АН | Alert Height | Высота сигнализации |
| АНР | Army Heliport | Военный вертопорт |
| AIC | Aeronautical Information Circular | Циркуляр аэронавигационной информации |
| AIP | Aeronautical Information Publication | Сборник аэронавигационной информации |
| AiRAC | Aeronautical Information Regulation and Control | Регламентирование и контроль аэронавигационной информации (АНИ) – Система заблаговременного уведомления об изменении АНИ по единой таблице дат вступления в силу |
| AIREP | Air-Report | Донесение. .с борта .с борта |
| AIS | Aeronautical Information Service | Служба аэронавигационной информации |
| ALA | Authorized Landing-Area | Разрешенная посадочная площадь (площадка) |
| ALF | Auxiliary Landing Field | Запасная посадочная площадка |
| ALS | Approach Light System | Система огней подхода |
| ALSF | Appoach Light System with Sequenced Flashing Lights | Система огней подхода с бегущими проблесковыми огнями |
| ALT | Altitude | Высота абсолютная |
| ALTN | Alternate | Запасной (аэродром) |
| AMA | Area Minimum Altitude | Минимальная абсолютная высота района |
| AMSL | Above Mean Sea Level | Над средним уровнем моря |
| AMSS | Aeronautical Mobil-Satellite Service | Авиационная подвижная спутниковая служба |
| ANGB | Air National Guard Base | Авиабаза (ВВС) национальной гвардии |
| AОС | Airport Obstacle Chart | Карта препятствий аэропорта |
| АОЕ | Airport/Aerodrome of Entry | Аэропорт/Аэродром входа |
| AOR | Area of Responsibility | Район ответственности |
| APAPI | Abbreviated Precision Approach Path Indicator | Упрощенный указатель траектории точного захода на посадку |
| АРС | Area Positive Control | Контролируемый район с эшелонированием |
| АРСН | Approach | Подход, заход на посадку |
| АРР | Approach Control | Контроль захода на посадку {диспетчерское обслуживание) |
| APRX | Approximate/ly | Приблизительный/о |
| APT | Airport | Аэропорт |
| ARB | Air Reserve Base | Резервная база ВВС |
| ARFF | Aircraft Rescue and Fire Fighting | Спасание воздушных судов и борьба с пожаром |
| ARINC | Aeronautical Radio Inc. | Объединение «Аэронавигационное радио» |
| ARO | ATS Reporting Office | Пункт сообщений ОВД |
| ARP | Airport Reference Point | Контрольная точка аэропорта |
| ARR | Arrival | Прибытие |
| ARSA | Airport Radar Service Area | Радиолокационное обслуживание в районе аэропорта |
| ARSR | Air Route Surveillance Radar | Маршрутный обзорный радиолокатор |
| ARTC | Air Route Traffic Control | Управление воздушным движением на трассе |
| ARTCC | Air Route Traffic Control Center | Центр управления воздушным движением на трассе |
| ASDA | Accelerate Stop Distance Available | Располагаемая дистанция прерванного взлета |
| ASE | Altimetry System Error | Погрешность системы измерения высоты |
| ASIR | Aviation Safety Incident Report | Отчет об инцидентах авиационной безопасности |
| ASL | Above Sea Level | Над уровнем моря |
| ASM | Air Space Managment System | Организация воздушного пространства |
| ASOS | Automated Surface Observation | Автоматизированная система наземного наблюдения (за погодой) |
| ASR | Airport Surveillance Radar | Обзорный радиолокатор аэропорта |
| АТА | Actual Time of Arrival | Фактическое время прилета |
| АТС | Air Traffic Control | Управление воздушным движением |
| АТСАА | Air Traffic Control Assigned Airspase | Воздушное пространство, контролируемое (службой) УВД |
| АТСС | Air Traffic Control Center | Центр управления воздушным движением |
| АТСТ | Air Traffic Control Tower | Вышка управления воздушным движением |
| ATD | Actual Time of Departure | Фактическое время вылета |
| ATF | Aerodrome Traffic Frequency | Частота аэродромного движения |
| ATFM | Air Traffic Flow Management | Управление потоками воздушного движения |
| ATIS | Automatic Terminal Information Service | Служба автоматической передачи информации в районе аэроузла (аэропорта) |
| ATM | Air Traffic Managment | Организация воздушного движения |
| ATS | Air Traffic Service | Обслуживание воздушного движения |
| AT-VAS1 | Abbreviated Tee Visual Approach Slope Indicator | Сокращенный Т-образный указатель визуальной глиссады захода на посадку |
| ATZ | Aerodrome Traffic Zone | Зона аэродромного движения |
| AUTH | Authorized | Разрешенный, уполномоченный |
| AUW | All-up Weight | Полная полетная масса |
| AUX | Auxiliary | Вспомогательный |
| AVASI | Abbreviated Visual Approach Slope Indicator | Упрощенный указатель визуальной глиссады захода на посадку |
| AVBL | Available | Наличный, имеющийся в распоряжении, действующий |
| AWIB | Aerodrom Weather Information Broadcast | Передача метеоинформации на аэродроме |
| AWOS | Automated Weather Observing System | Автоматизированная система наблюдения за погодой |
| AWY | Airway | Воздушная трасса |
| AZM | Azimuth | Азимут |
| BARO-VNAV | Barometric-Vertical Navigation | Вертикальная навигация по барометрическому высотомеру ВС |
| BC | Back Course | Обратный путевой угол (для ILS обратный курсовой луч) |
| BCM | Back Course Marker | Маркер обратного курсового луча (ILS) |
| BCN | Beacon | Маяк |
| BCST | Broadcast | Радиовещание |
| BDRY | Boundary | Граница |
| BLDG | Building | Здание |
| ВМ | Back Marker | Обратный маркер |
| BRG | Bearing | Пеленг |
| B-RNAV | Basic Area Navigation | Зональная навигация — основной метод |
| BS | Broadcast Station (Commercial) | Радиовещательная станция (коммерческая) |
| BTN | Between | Между |
| АТС IFR | Flight Plan Clearance Delivery Frequency | Частота передачи диспетчерского разрешения на план полета по ППП |
| CADIZ | Canadian Air Defense Identification Zone | Канадская зона опознавания ПВО |
| CALC | Calculator | Калькулятор |
| CARS | Community Aerodrome Radio | Аэродромная радиостанция связи Station |
| CAS | Collision Avoidance System | Система предотвращения столкновения |
| CAT | Category | Категория |
| Ccw | Counterclockwise | Против часовой стрелки |
| CDR | Conditional Route | Условный маршрут |
| CDT | Central Daylight Time | Центральное дневное время (США) |
| CEIL | Ceiling | Потолок, нижняя граница облачности |
| CEU | Central Executive Unit | Центральный исполнительный орган |
| CERAP | Combined Center/Radar Approach Control | Объединенный центр/ Радиолокационное управление заходом на посадку |
| CFL | Cleared Flight Level | Разрешенный эшелон полета |
| CFMU | Central Flow Management Unit | Центральный орган организации потоков |
| CGAS | Coast Guard Air Station | Авиационная станция береговой охраны |
| CGL | Circling Guidance Lights | Вращающиеся огни наведения |
| СН | Channel | Канал, линия связи, полоса частот |
| СН | Critical Height | Критическая высота |
| CL | Runway Centerline Lights | Осевые огни ВПП |
| CMNPS | Canadian Minimum Navigation Performance Specification | Канадские технические требования к минимальным навигационным характеристикам |
| CMV | Converted Met Visibility | |
| CNS | Communication, Navigation and Surveillance | Связь, навигация и наблюдение |
| СО | County | Округ (США), графство (Англия) |
| COMM | Communications | Сообщение, связь |
| COMSND | Commissioned | Введено в эксплуатацию, укомплектовано |
| CONT | Continuous | Непрерывный, сплошной |
| COORD | Coordinates | Координаты |
| СОР | Change Over Point | Точка переключения (частоты) |
| CORR | Corridor | Коридор |
| CP | Command Post | Командный пункт |
| CPDLC | Controller/Pilot data link | Связь «диспетчер/пилот» по линии передачи данных |
| Cpt | Clearance (Pre-Taxi Procedure) | Разрешение (перед выруливанием) |
| CRAM | Conditional Route Availability Message | Сообщение о годности условного маршрута |
| CRP | Compulsory Reporting Point | Пункт обязательного донесения |
| CRS | Course | Направление полета, заданный путевой угол, заданное направление |
| C/S | Call Sign | Позывной |
| CST | Central Standard Time | Центральное стандартное время (США) |
| СТА | Control Area | Диспетчерский район |
| CTAF | Common Traffic Advisory Frequency | Общая консультативная частота обслуживания воздушного движения |
| CTL | Control | Контроль, диспетчерское обслуживание |
| CTR | Control Zone | Диспетчерская зона |
| CVFR | Controlled VFR | Контролируемый полет по ПВП |
| CVSM | Conventional Vertical Separation Minimum | Традиционный минимум вертикального эшелонирования |
| CW | Clockwise | По часовой стрелке |
| CWY | Clearway | Полоса свободная от препятствий |
| D | Day | День |
| DA | Decision Altitude | Абсолютная высота принятия решения |
| DA (Н) | Decision Altitude (Height) | Абсолютная (относительная) высота принятия решения |
| DCT | Direct | Прямо |
| DECMSND | Decommissioned | Снят с эксплуатации |
| DEG | Degree | Градус |
| DER | Departure End of Runway | Взлетный конец ВПП |
| DEWIZ | Distance Early Warning Identification Zone | Зона раннего опознавания ПВО |
| DF | Direction Finder (Finding) | Пеленгатор (пеленгование) |
| DH | Decision Height | Относительная высота принятия решения |
| DIR | Director | «Наведение» (частота связи) |
| DiSPL THRESH | Displaced Threshold | Смещенный порог (ВПП) |
| DIS, DIST | Distance | Расстояние |
| DLY | Daily | Ежедневно |
| DME | Distance-Measuring Equipment | Дальномерное оборудование |
| DOD | Department of Defense | Департамент обороны |
| DOM | Domestic | Внутренний |
| DOP | Dilution of Precision | Снижение точности |
| DR | Dead Reckoning Position | Место, определяемое счислением пути |
| DTK | Desired Track | Заданный путевой угол |
| DTW | Dual Tandem Wheel Landing | Шасси — двойной тандем Gear |
| DVOR | Doppler VOR | Доплеровский VOR |
| DW | Dual Wheel Landing Gear | Шасси — спаренные колеса |
| E | East or Eastern | Восток или восточный |
| EAT | Expected Approach Time | Прёдпологаемое время захода на посадку |
| ЕСАС | European Civil Aviation Conference | Европейская конференция гражданской авиации |
| ECOMS | Jeppesen explanation of Common Minimum Specifications | Объяснения «Джеппсен» по общим характеристикам минимумов |
| EDT | Eastern Daylight Time | Восточное дневное время (США) |
| EDPS | Flight Data Processing System | Система обработки полетных данных |
| EET | Estimated Elapsed Time | Расчетное истекшее время |
| EGPWS | Enhance Ground Proximity Warning System | Система сигнализации об опасности сближения с землей (СРППЗ) с расширенными возможностями |
| EFAS | Enroute Flight Advisory Service | Консультативное обслуживание полета на мар¬шруте |
| EFF | Effective | Вступивший в силу, действующий |
| ELEV | Elevation | Превышение |
| EMERG | Emergency | Авария, аварийная ситуация |
| ENG | Engine | Двигатель |
| ЕОВТ | Estimated off block time | Расчетное время начала движения |
| EST | Eastern Standard Time | Восточное стандартное время (США) |
| ЕТА | Estimated Time of Arrival | Расчетное время прибытия |
| ETD | Estimated Time of Departure | Расчетное время вылета |
| ETE | Estimated Time Enroute | Расчетное время в пути |
| ETOPS | Extended Range Operation with two engine airplanes | Полет увеличенной дальности действия ВС с двумя двигателями |
| EXC | Except | За исключением |
| F | Condenser Discharge Sequential Flashing Lights/Sequenced Flashing Lights | Газоразрядные бегущие проблесковые огни/Бегущие проблесковые огни |
| FAA | Federal Aviation Administration | Федеральная авиационная администрация |
| FAC | Final Approach Course | Направление конечного этапа захода на посадку |
| FAF | Final Approach Fix | Контрольная точка конечного этапа захода на посадку |
| FANS | Future Air Navigation System | Комитет IСАО по будущим навигационным системам |
| FAP | Final Approach Point | Точка конечного этапа захода на посадку |
| FAR | Federal Aviation Regulation | Федеральные авиационные правила (США) |
| FAS | Final Approach Segment | Участок конечного этапа захода на посадку |
| FCP | Final Control Point | Контролируемая точка на последней прямой |
| FDPS | Flight Data Processing System | Система обработки полетных данных |
| FDE | Fault Detection and Exclusion | обнаружение неисправностей и исключение |
| FIC | Flight Information Center | Центр полетной информации |
| FIR | Flight Information Region | Район полетной информации |
| FIS | Flight Information Service | Полетно-информационное обслуживание, Служба полетной информации |
| FL | Flight Level (Altitude) | Эшелон полета (Абсолютная высота) |
| FLAS | Flight Level Allocation Scheme | Схема распределения эшелонов полета |
| FLD | Field | Аэродром (грунтовый) |
| FLG | Flashing | Проблесковый, мигающий |
| FLP | Flight Plan | План полета |
| FLT | Flight | Полет, рейс |
| FM | Fan Marker | Веерный маркер |
| FMCS | Flight Managment Computer Syatem | Компьютерная система управления полетом |
| FMS | Flight Management System | Система управления полетом |
| FPL | Flight Plan (АТС) | План полета (для УВД) |
| FPM | Feet Per Minute | Футов в минуту |
| FPR | Flight Planning Requirement | Требования по планированию полета |
| FREQ | Frequency | Частота |
| FSS | Flight Service Station | Станция полетного обслуживания |
| FT | Feet | Футы |
| FTE | Flight Technical Error | Погрешность, обусловленная техникой пилотирования |
| FTS | Flexible Track System | Система изменяемых треков |
| FUA | Flexible Use of Airspace | Гибкое использование воздушного пространства |
| G | Guards only (radio frequencies) | Только прослушивание (радиочастот) |
| GA | General Aviation | Авиация общего назначения |
| GAL | Gallons | Галлоны |
| GAT | General Air Traffic | Общее воздушное движение |
| GCA | Ground Controlled Approach (radar) | Заход на посадку по командам с земли (по локатору) |
| GDOP | Geometric Dilution of Precision | Геометрическое снижение точности |
| GEO | Geographic or True | Географический или истинный |
| GLONASS | Global Orbiting Navigation Satellite System | Глобальная орбитальная навигационная спутниковая система |
| GLS | GNSS Landing System | Посадочная система глобальной навигационной спутниковой системы |
| GMT | Greenwich Mean Time | Гринвичевское среднее время |
| GND | Ground Control | Управление наземным движением (диспетчер руления) |
| GND | Surface of the Earth (either land or water) | Поверхность земли (суши или воды) |
| GNSS | Global Navigation Satellite System | Глобальная навигационная спутниковая система |
| GP | Glidepath | Глиссада |
| GPS | Global Positioning System | Глобальная система определения местоположения |
| GPWS | Ground Proximity Warning System | Система сигнализации об опасности сближения с землей |
| GRS | Ground Reference Station | Наземная опорная станция |
| GRVD | Grooved | Покрытие с желобками |
| GS | Glide Slope | Глиссада планирования |
| G/S | Ground Speed | Путевая скорость |
| GWT | Gross Weight | Общая масса |
| Н | Non-Directional Radio Beacon ог High Altitude | Ненаправленный радиомаяк или высота в верхнем воздушном пространстве |
| Н24 | 24 Hour Service | Круглосуточная работа |
| НАА | Height Above Airport | Относительная высота над аэро-дромом |
| HAT | Height Above Touchdown | Относительная высота над зоной приземления |
| НС | Critical Height | Критическая высота |
| HDG | Heading | Курс |
| HDOP | Horizontal Dilution of Precision | Снижение точности определения местоположе¬ния по горизонтали |
| HEL | Helicopter | Вертолет |
| HF | High Frequency (3 — 30 MHz) | Высокая частота (3 — 30 МГц) |
| НОТ | Height | Высота относительная |
| HI | High (altitude) | Большая (абсолютная) высота, верхнее воздушное пространство |
| HI | High Intensity (lights) | Высокая интенсивность (огней) |
| HIALS | High Intensity Approach Light System | Система огней подхода высокой интенсивности |
| HIRL | High intensity Runway Edge Lights | Посадочные боковые огни ВПП высокой интенсивности |
| HIWAS | Hazardous inflight Weather Advisory Service | Консультативное оповещение об опасных явлениях погоды в полете |
| HJ | Sunrise to Sunset | От восхода до захода СоЛнца |
| HN | Sunset to Sunrise | От захода до восхода Солнца |
| НО | By Operational Requirements | По эксплуатационным требованиям |
| hPa | Hectopascal (one hectopascal = one millibar) | Гектопаскаль (1 гектопаскаль = 1 миллибару) |
| HR | Hours (period of time) | Часы (период времени) |
| HS | During Hours of Scheduled Operations | В часы полетов по расписанию |
| HSI | Horizontal Situation Indicator | Индикатор горизонтальной обстановки, плановый навигационный прибор |
| HST | High Speed Taxi-way Turn-off | Скоростная РД для сруливания |
| HTZ | Helicopter Traffic Zone | Зона полетов вертолетов |
| HWP | Holding Way Point | Точка зоны ожидания (RNAV) |
| Hz | Hertz (cycles per second) | Герц (периодов в секунду) |
| I | Island | Остров |
| IAC | Instrument Approach Chart | Карта захода на посадку по приборам |
| IAF | Initial Approach Fix | Контрольная точка начального этапа захода на посадку |
| IAP | Instrument Approach Procedure | Процедура (схема) захода на посадку по приборам |
| IAS | Indicated Airspeed | Приборная воздушная скорость |
| IBN | identification Beacon | Опознавательный маяк |
| ICAO | International Civil Aviation Organization | Международная организация гражданской авиации (ИКАО) |
| IDENT | Identification | Опознавание |
| IF | Intermediate Fix | Контрольная точка промежуточного (этапа захода на посадку) |
| IFF | Identification Friend or Foe | Опознавание «свой — чужой» |
| IFR | Instrument Flight Rules | Правила полетов по приборам |
| IGS | Instrument Guidance System | Система наведения по приборам |
| ILS | Instrument Landing System | Система посадки по приборам |
| IM | inner Marker | Ближний (внутренний) маркер/привод |
| IMC | Instrument Meteorological Conditions | Приборные метеорологические условия |
| IMS | Integrity Monitoring System | Система контроля целостности |
| IMTA | Intensive Military Training Area | Район интенсивных военных тренировочных по¬летов |
| INBD | Inbound | (Полет) «на» . .., прибывающий, прилетающий .., прибывающий, прилетающий |
| INDEFLY | Indefinitely | Неопределенно |
| IN or INS | Inches | Дюймы |
| INFO | Information | Информация |
| INOP | Inoperative | Недействующий |
| INP | If Not Possible | Если невозможно |
| INS | Inertial Navigation System | Инерциальная навигационная система |
| INT | Intersection | Пересечение |
| INTL | International | Международный |
| IORRA | Indian Ocean Random RNAV Area | Произвольный район зональной навигации Индийского океана |
| IR | Instrument Restricted Controlled Airspace | Контролируемое воздушное пространство, ограниченное для полетов по ППП |
| IS | islands | Острова |
| ITWS | Integrated Terminal Weather System | Объединенная метеорологическая система аэроузла |
| I/V | Instrument/Visual Controlled Airspace | Контролируемое воздушное пространство для полетов по ППП/ПВП |
| JAA | Joint Aviation Authorities | Объединенная авиационная администрация (стран Западной Европы) |
| JAA AMC | JAA Acceptable Means of Compliance | Приемлемые средства соответствия JAA |
| JAR | Joint Aviation Requirements | Объединенные авиационные требования |
| JBD | James Brake Decelerometer (Canada) | Измеритель коэффициента сцепления по Джеймсу (Канада) |
| JBI | James Brake Index (Canada) | Индекс коэффициента сцепления по Джеймсу (Канада) |
| KGS | Kilograms | Килограммы |
| kHz | Kilohertz | Килогерц |
| KIAS | Knots Indicated Airspeed | Приборная скорость в узлах |
| КМ | Kilometers | Километры |
| KMH | Kilometer(s) per Hour | Км/ч |
| KT | Knots | Узлы |
| KTAS | Knots True Airspeed | Истинная воздушная скорость в узлах |
| L | Locator (Compass) | Привод |
| LAA | Local Airport Advisory | Консультативное обслуживание в местном аэропорту |
| LAAS | Local Area Augmentation System | Система функционального дополнения с ограничейной зоной действия |
| LAHSO | Land and Hold Short Operations | Операции: посадка и кратковременное ожидание |
| LAL | Level Alarm Low – как вариант | |
| LAT | Latitude | Широта |
| LBCM | Locator Back Course Marker | Приводная радиостанция обратного курса (по¬садки) с маркером |
| LAD GNSS | Landing GNSS | Локальная дифференциальная GNSS |
| IBM | Locator Back Marker | Приводная радиостанция обратного маркера |
| LBS | Pounds (Weight) | Фунты (вес) |
| LC | Landing Chart | Карта посадки |
| LCG | Load Classification Group | Классификационная группа нагрузки |
| LCN | Load Classification Number | Классификационное число нагрузки |
| Lctr | Locator (Compass) | Привод |
| LDA | Landing Distance Available | Располагаемая посадочная дистанция |
| LDA | Localizer type Directional Aid | Средство наведения типа курсового маяка |
| LDI | Landing Direction Indicator | Указатель направления посадки |
| LDIN | Lead-in Light System | Система ведущих (посадочных) огней |
| LGTH | Length | Длина |
| LH | Left Hand | Левостороннее (движение) |
| LIM | Locator Inner Marker | Привод внутреннего маркера |
| LLWAS | Low Level Wind Shear Alert System | Система предупреждения о сдвиге ветра на низких высотах |
| LMM | Locator Middle Marker | Привод среднего маркера |
| LNDG | Landing | Приземление, посадка |
| LNAV/VNAV | Lateral Navigation/Vertical Navigation | Навигация по направлению / Навигация по вертикали |
| LO | Locator at Outer Marker Site | Приводная радиостанция, совмещенная с вне¬шним маркером |
| LOC | Localizer (Jeppesen abbreviation) | Курсовой радиомаяк (аббревиатура «Джеппсен») |
| LOG | Locator (ICAO abbreviation, not used by Jeppesen) | Приводная радиостанция (аббревиатура ИКАО не используется «Джеппсен») |
| LOM | Locator Outer Marker | Привод внешнего маркера |
| LONG | Longitude | Долгота |
| LSALT | Lowest Safe Altitude | Наименьшая безопасная абсолютная высота |
| LT | Local Time | Местное время |
| LTS | Lights | Огни |
| LVP | Low Visibility Procedures | Процедуры при низкой видимости |
| М | Meters | Метры |
| МАА | Maximum Authorized Altitude | Максимальная разрешенная абсолютная вы¬сота |
| MAG | Magnetic | Магнитный |
| MALS | Medium Intensity Approach Light System | Система огней подхода средней интенсивности |
| MALSF | Medium Intensity Approach Light System with Sequenced Flashing Lights | Система огней подхода средней интенсивности с бегущими проблесковыми огнями |
| MALSR | Medium Intensity Approach Light System with Runway Alingment Indicator Lights | Система огней подхода средней интенсивности с индикатором огней створа ВПП |
| MAP | Missed Approach Point | Точка ухода на повторный заход |
| MASPS | Minimum Aircraft System Performance Specification | Технические требования к минимальным характеристикам бортовых систем |
| МАХ | Maximum | Максимум, максимальный |
| MB | Millibars | Миллибары |
| МВОН | Minimum Break Off Height | Минимальная относительная высота отключения (автоматики на переход к ручному пилотированию) |
| MBZ | Mandatory Broadcast Zone | Зона обязательной передачи (радиосигнала) |
| МСА | Minimum Crossing Altitude | Минимальная абсолютная высота пересечения |
| MCAF | Marine Corps Air Facility | Аэронавигационное средство морской пехоты |
| MCAS | Marine Corps Air Station | Авиабаза морской пехоты |
| МСОМ | Multicom | Оперативное обслуживание для определенного круга абонентов, используемое с целью обес¬печения необходимой связи при использова¬нии ВПП для уменьшения задержки и увеличе¬ния ее пропускной способности |
| МСТА | Military Controlled Airspace | Воздушное пространство, контролируемое военными |
| MDA | Minimum Descent Altitude | Минимальная абсолютная высота снижения |
| MDA (H) | Minimum Descent Altitude (Height) | Минимальная абсолютная (относительная) высота снижения |
| MDT | Mountain Daylight Time | Горное дневное время (США) |
| MEA | Minimum Enroute Altitude | Минимальная абсолютная высота по маршруту |
| МЕНТ | Minimum Eye Height Over Threshold | Минимальная высота глаза (наблюдателя) над порогом (ВПП) |
| MEML | Memorial | Мемориал, мемориальный |
| МЕТ | Meteorological | Метеорологический |
| MF | Mandatory Frequency | Обязательная частота |
| МНА | Minimum Holding Altitude | Минимальная абсолютная высота ожидания |
| MHz | Megahertz | Мегагерц |
| Ml | Medium Intensity (lights) | Средней интенсивности (огни) |
| MiALS | Medium Intensity Approach Light System | Система огней подхода средней интенсивноети |
| MIL | Military | Военный |
| MIM | Minimum | Минимум, минимальный |
| MIN | Minute | Минута |
| MIRL | Medium Intensity Runway Edge Lights | Посадочные боковые огни ВПП средней интенсивности |
| MKR | Marker Radio Beacon | Маркерный радиомаяк |
| MLS | Microwave Landing System | Микроволновая система посадки |
| MLW | Maximum Certificated Landing Weight | Максимальная сертифицированная посадочная масса |
| MM | Middle Marker | Средний маркер |
| MNPS | Minimum Navigation Performance Specifications | Технические требования к минимальным навигационным характеристикам |
| МОА | Military Operation Area | Район военных операций |
| МОСА | Minimum Obstruction Clearance Altitude | Минимальная абсолютная высота пролета препятствий |
| MOPS | Minimum Operational Performance Specification | Стандарты минимальных эксплуатационных характеристик |
| MORA | Minimum Off-Route Altitude (Grid or Route) | Минимальная абсолютная высота вне маршрута (сеточная или маршрутная) |
| MPS | Meters per Second | Метры в секунду |
| MPW | Maximum Permitted Weigh | Максимальный разрешенный вес |
| MRA | Minimum Reception Altitude | Минимальная абсолютная высота приема (сиг¬нала) |
| MSA | Minimum Safe Altitude | Минимальная безопасная абсолютная высота |
| MGS | Message | (Вывод) сообщение |
| MSL | Mean Sea Level | Средний уровень моря |
| MST | Mountain Standard Time | Горное стандартное время (США) |
| МТА | Military Training Area | Район военных тренировочных полетов |
| MTAF | Mandatory Traffic Advisory Frequency | Предписанная частота для консультативного движения |
| МТСА | Minimum Terrain Clearance Altitude | Минимальная безопасная абсолютная высота над рельефом местности |
| МТМА | Military Terminal Control Area | Военный узловой диспетчерский район |
| MTOW | Maximum Take-off Weight | Максимальная взлетная масса |
| MTWA | Maximum Total Weight Authorized | Максимальная разрешенная общая масса |
| MUN | Municipal | Муниципальный (городской) |
| MVA | Minimum Vectoring Altitude | Минимальная абсолютная высота векторения |
| MVFR | Marginal VFR | ПВП в особых условиях |
| N | Night, North or Norhern | Ночь, север или северный |
| NA | Not Authorized | He разрешено |
| NAAS | Naval Auxiliary Air Station | Военно-морская вспомогательная авиастанция |
| NADC | Naval Air Development Center | Авиационный научно-исследовательский центр ВМС |
| NAEC | Naval Air Engineering Center | Авиационно-технический центр ВМС |
| NAF | Naval Air Facility | Военно-морские авиационные навигационные (радио)средства |
| NALF | Naval Auxiliary Landing Field | Вспомогательное посадочное поле ВМС |
| NAP | Noise Abatement Procedure | Процедура уменьшения шума |
| NAR | North American Routes | Северо-Американские маршруты |
| NAS | Naval Air Station | Авиастанция ВМС |
| NAT | North Atlantic Traffic | Полеты в Северной Атлантике |
| NAT/OTS | North Atlantic Traffic/Organized Track System | Полеты в Северной Атлантике / Система организованных треков |
| NATL | National | Национальный |
| NAV | Navigation | Навигация |
| NAVAID | Navigational Aid | Навигационное средство |
| NCA | Northern Control Area | Северный диспетчерский район |
| NCRP | Non-Compulsory Reporting Point | Пункт необязательного доклада |
| NDB | Non-Directional Beacon / Radio Beacon | Ненаправленный радиомаяк / Радиомаяк |
| NE | Northeast | Северо-восток |
| NM | Nautical Mile(s) | Морская миля(и) |
| No | Number | Число, номер |
| NoPT | No Procedure Turn | Процедура стандартного разворота не требуется |
| NOTAM | Notices to Airmen | Извещения для летчиков |
| NSE | Navigation System Error | Погрешность навигационной системы |
| NW | Northwest | Северо-запад |
| NWC | Naval Weapons Center | Военно-морской центр вооружения |
| О/А | On or About | «На» или «около» |
| ОАС | Oceanic Area Control | Диспетчерское обслуживание в океаническом Районе |
| OAT | Operational air traffic | Оперативное воздушное движение |
| OBS | Omnidirectional Bearing Selected | Заданное (выбранное) направление (пеленг) выхода в пункт маршрута |
| ОСА | Oceanic Control Area | Океанический диспетчерский район |
| ОСА (Н) | Obstacle Clearance Altitude (Height) | Абсолютная (относительная) высота пролета препятствий |
| OCL | Obstruction Clearance Limit | Запас высоты пролета препятствия |
| OCNL | Occasional | Нерегулярный |
| ОСТА | Oceanic Control Area | Океанический диспетчерский район |
| ODALS | Omni-Directional Approach Light System | Система всенаправленных огней подхода |
| ОМ | Outer Marker | Внешний маркер |
| OPS | Operations or Operates | Работы, эксплуатации, полеты или работает, эксплуатирует, выполняет полет |
| O/R | On Request | По запросу |
| О/Т | Other Times | В другое время |
| OTS | Out-of-Service | Неисправен, не работает, обслуживание не предоставляется |
| OTS | Organized Track System | Система организованных треков |
Общий анализ мочи при цистите
Цистит часто встречаемое воспалительное заболевание мочевого пузыря среди взрослого населения, особенно у женщин. Острый цистит может переходить в хроническую форму с периодическими обострениями. Причинами частых обострений цистита у женщин являются короткая, широкая уретра (мочеиспускательный канал) и близость к естественным источникам инфекции – влагалище и анус. Гормональные нарушения у женщины часто приводят к дисбиозу влагалища и росту патогенных бактерий, которые являются провокатором частых обострений воспаления мочевого пузыря. У мужчин симптомы цистита как правило связаны с заболеванием предстательной железы.
Острый цистит может переходить в хроническую форму с периодическими обострениями. Причинами частых обострений цистита у женщин являются короткая, широкая уретра (мочеиспускательный канал) и близость к естественным источникам инфекции – влагалище и анус. Гормональные нарушения у женщины часто приводят к дисбиозу влагалища и росту патогенных бактерий, которые являются провокатором частых обострений воспаления мочевого пузыря. У мужчин симптомы цистита как правило связаны с заболеванием предстательной железы.
Основные симптомы цистита
- частое болезненное мочеиспускание
- боль в паховой области
- ложные позывы к мочеиспусканию
- мутная моча, возможно появление примеси крови
- внезапное начало симптомов
- повышение температуры тела
Какой анализ мочи нужен при цистите
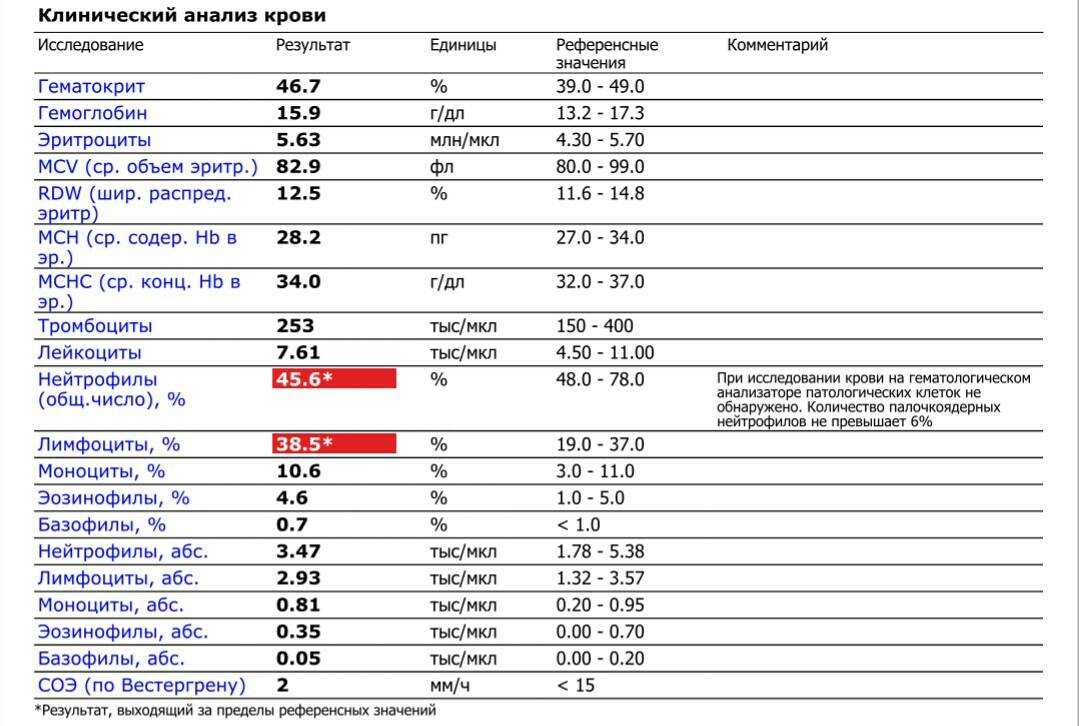
При подозрении на цистит сначала обязательно нужно сдать общий анализ мочи (ОАМ). В результатах ОАМ при цистите будет выявлено повышенное содержание лейкоцитов, бактерий, может встречаться повышенное содержание эритроцитов и белка.
Дополнительно лечащий врач может рекомендовать провести бактериальный посев мочи с определением антибиотикочувствительности к выявленным патогенным микроорганизмам, ПЦР диагностику на заболевания, передающиеся половым путем, ряд исследований на диагностику вирусных инфекций (так как не всегда причиной цистита являются бактерии).
Из инструментальных исследований врач может направить пациента на УЗИ почек, КТ/МРТ малого таза для исключения опухолей и камней в мочевыделительной системе, заболеваний почек и предстательной железы у мужчин.
Профилактика обострений цистита
- Регулярно проводить тщательный туалет наружных половых органов
- Использовать барьерные способы контрацепции
- Своевременно проводить лечение гинекологических и урологических заболеваний
- В течение ближайшего времени после полового акта помочиться
Подготовка к сдаче ОАМ при цистите
В день перед взятием биоматериала желательно воздержаться от физических нагрузок, приема алкоголя, не употреблять в пищу овощи и фрукты (свеклу, морковь, цитрусовые, арбузы), красное вино, поливитамины, которые могут изменить цвет мочи.
Исключить прием мочегонных препаратов в течение 48 часов до сбора мочи (согласовывается с лечащим врачом).
Собирать мочу нужно до начала антибиотикотерапии.
Провести тщательный туалет наружных половых органов под душем с мылом (запрещается использовать гигиенические средства с антисептиками). Мужчинам оттянуть крайнюю плоть пениса, хорошо обмыть головку теплой водой, просушить бумажным полотенцем.
Женщины во время менструации перед сбором мочи должны поставить во влагалище тампон и сообщит лечащему врачу, что анализ проведен во время менструации.
Как правильно собирать анализ мочи при цистите
В стерильный контейнер собирается средняя порция мочи при первом утреннем мочеиспускании (первая и последние порции сливаются в унитаз).
Возможен сбор мочи в любое время в течение дня по предварительному согласованию с лечащим врачом.
Во время сбора мочи желательно не касаться контейнером тела.
Перед началом мочеиспускания женщинам нужно развести пальцами половые губы пальцами, чтобы с кожи наружных половых органов в мочу не попали посторонние примеси.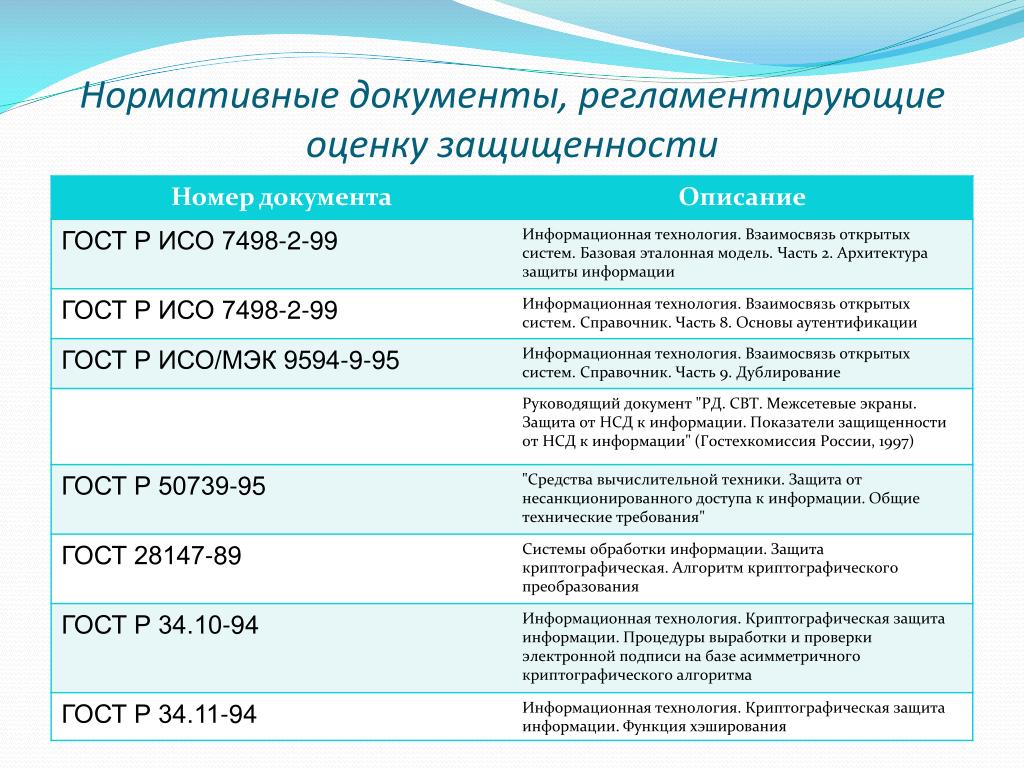
Объем мочи для исследования должен составлять ¾ объема контейнера. Минимальный объем мочи для исследования составляет 30 мл.
Доставить контейнер с мочой в медицинский офис желательно в течение 2-х часов после сбора биоматериала.
Что показывает анализ мочи при цистите
ОАМ позволяет увидеть общую картину воспаления. Для постановки диагноза во внимание в первую очередь учитываются жалобы пациента. ОАМ нужен для подтверждения диагноза, основанного на клинической картине, так как болезненность при мочеиспускании может встречаться у пациентов с нарушением нервной регуляции акта мочеиспускания, без цистита.
Расшифровка общего анализа мочи при цистите
Необходимо помнить, что расшифровка результатов исследования мочи должна проводиться только лечащим врачом, так как результаты лабораторных исследований не являются единственным критерием, для постановки диагноза и назначения соответствующего лечения. Они должны рассматриваться в комплексе с данными анамнеза и результатами других возможных обследований, включая инструментальные методы диагностики.
В медицинской компании «LabQuest» Вы можете получить персональную консультацию врача службы «Doctor Q» по расшифровке результатов исследования мочи во время приема или по телефону.
Цвет. В норме цвет желтый различной насыщенности. Он может меняться при употреблении некоторых продуктов и приеме ряда лекарственных препаратов. Белесый, темно-бурый или другой нехарактерный цвет указывает на наличие патологии. Моча должна быть прозрачной.
Запах аммиака, гниющих яблок или тухлого мяса указывает на различные заболевания (например, цистит, сахарный диабет, гнойное воспаление).
Реакция мочи. В норме рН составляет 5-7 (слабокислая реакция). Повышенная кислотность характерна для лихорадочных состояний, почечной недостаточности, сахарного диабета и других патологий. Щелочная реакция наблюдается при хронических инфекционных заболеваниях.
Показатели плотности используются для оценки функций почек. В течение суток удельный вес мочи колеблется.
Белок в моче (протеинурия) в норме отсутствует. Его появление – маркер наличия различных заболеваний (воспалительные инфекционные заболевания мочевыводящих путей, патология почек и другие). Также белок определяется в моче после сильного переохлаждения, высокой физической нагрузки.
Его появление – маркер наличия различных заболеваний (воспалительные инфекционные заболевания мочевыводящих путей, патология почек и другие). Также белок определяется в моче после сильного переохлаждения, высокой физической нагрузки.
Глюкозы в норме в моче быть не должно. Ее выявление в образце биоматериала может свидетельствовать как о наличии заболеваний (сахарный диабет, онкология поджелудочной железы, панкреатит и прочее), так и о сильном стрессе, употреблении в пищу большого количества углеводов.
Билирубин выявляется при гепатитах, циррозе, механической желтухе и других патологических состояниях, связанных с повреждениями печени.
Уробилиноген в высокой концентрации указывает на поражения печени, гемолитическую желтуху, заболевания ЖКТ. Повышенное количество кетоновых тел свидетельствует о нарушении белкового, углеводного или липидного обмена. Нитриты указывают на инфекцию мочевыводящих путей.
Плоский эпителий – это поверхностно расположенные клетки кожи наружных половых органов. Обнаружение его в моче диагностического значения не имеет.
Обнаружение его в моче диагностического значения не имеет.
Переходный эпителий находится в почках, мочеточниках, мочевом пузыре и верхнем отделе мочеиспускательного канала. Единичные клетки могут встречаться в осадке мочи у здоровых людей. В большом количестве обнаруживаются при интоксикации, после инструментальных вмешательств на мочевыводящих путях, при желтухах, почечнокаменной болезни и хроническом цистите.
Почечный эпителий у здоровых людей в микроскопии осадка не встречается. Обнаруживается у пациентов с нефрозами и нефритами.
Эритроциты в норме присутствуют в моче в незначительном количестве. Небольшое количество эритроцитов может наблюдаться после спортивных нагрузок, травмах поясницы, при переохлаждении и перегревании. Появление большого количества эритроцитов в моче может встречаться при различных патологиях (гломерулонефриты, нефрозы, коллагенозы, заболевания сердца, сепсис, грипп, инфекционный мононуклеоз, краснуха, ангина, дизентерия и др.).
Лейкоциты присутствуют в моче здоровых людей. Повышенное количество лейкоцитов в моче у женщин может встречаться при контаминации мочи влагалищными выделениями. Высокое содержание лейкоцитов в моче бывает при пиелоциститах, пиелонефритах, при лихорадке различного генеза, инфекциях мочеполовых путей.
Повышенное количество лейкоцитов в моче у женщин может встречаться при контаминации мочи влагалищными выделениями. Высокое содержание лейкоцитов в моче бывает при пиелоциститах, пиелонефритах, при лихорадке различного генеза, инфекциях мочеполовых путей.
Цилиндры — образования цилиндрической формы, которые в основном состоят из белка и/или клеток. Встречаются как правило при патологии мочевыделительной системы (гломерулонефрит, пиелонефрит, туберкулез почек, диабетическая нефропатия, хроническая почечная болезнь, амилоидоз почек, лихорадка, скарлатина, миеломная болезнь, остеомиелит, системная красная волчанка и пр.).
Слизь выполняет защитную функцию, выделяется специальными клетками мочеполовой системы. В норме ее содержание в моче незначительное, при воспалительных процессах может увеличивается.
Кристаллы солей появляются в зависимости от рН мочи и других ее свойств, рациона питания. Могут указывать на нарушения минерального обмена, наличие камней или повышенный риск развития мочекаменной болезни.
Бактерии указывают на бактериальную инфекцию мочевыделительного тракта. Но могут встречаться при контаминации мочи бактериями с кожных покровов и из влагалищных выделений.
Где можно сдать анализ мочи при цистите
Сдать ОАМ при цистите можно в ближайшем медицинском офисе лаборатории «LabQuest». Список медицинских офисов, где принимается биоматериал, представлен в разделе «Адреса и время работы».
158876 просмотров
Автор-врач: Савченко Светлана Петровна
Эксперт в области лабораторной диагностики, организации здравоохранения, диагностики и лечения заболеваний терапевтического профиля.
Дата публикации статьи: 12.01.2021
Обновлено: 19.08.2022
WMS система управления складом — что это
WMS система управления складом — что это- Главная
- Отрасли
- WMS
WMS-система управления складом (Warehouse Management System) – это мощный программный инструментарий, предназначенный для автоматизации управления процессами склада или работы складского комплекса. Функционал системы управления складом позволяет пользователю централизованно, под управлением WMS-программы, с применением мобильных и голосовых терминалов выполнять складские операции. Эксплуатация склада с внедренной WMS-системой осуществляется просто и эффективно, позволяя свести к минимуму потери при выполнении складских операций.
Функционал системы управления складом позволяет пользователю централизованно, под управлением WMS-программы, с применением мобильных и голосовых терминалов выполнять складские операции. Эксплуатация склада с внедренной WMS-системой осуществляется просто и эффективно, позволяя свести к минимуму потери при выполнении складских операций.
В этой статье мы расскажем о WMS системе управления складом и о всех критически важных бизнес-процессах, связанных с управлением работой склада.
Рассмотрим такие аспекты управления логистикой склада, как:
- Что такое WMS-система управления складом;
- Какие преимущества внедрения системы управления складом;
- Функционал WMS-системы управления складом;
- Как выбрать систему управления складом.
Что такое WMS-система управления складом?
Система управления складом (WMS) – это программа, которая разработана для оптимизации процессов логистики склада, распределения, цепочки поставок и выполнения заказов. Обычно, система управления складом предоставляет функционал, помогающий упростить и улучшить логистику склада, начиная с момента поступления товара на склад и его приемки, и заканчивая отгрузкой заказчику. Одним из важных критериев WMS системы является способность к интеграции с другим программным обеспечением и бизнес-приложениями, что позволяет связывать и оптимизировать все процессы предприятия.
Обычно, система управления складом предоставляет функционал, помогающий упростить и улучшить логистику склада, начиная с момента поступления товара на склад и его приемки, и заканчивая отгрузкой заказчику. Одним из важных критериев WMS системы является способность к интеграции с другим программным обеспечением и бизнес-приложениями, что позволяет связывать и оптимизировать все процессы предприятия.
Преимущества внедрения WMS-системы управления складом:
Внедрение системы управления складом (WMS-логистика склада) дает бизнесу огромные преимущества, начиная от возможности быстрого принятия решений на основе предоставляемых данных и до значительного сокращения издержек при выполнении заказов и затрат на их обработку.
Рассмотрим основные преимущества:
Наличие исчерпывающих актуальных данных для принятия быстрых решений
Система управления складом отражает всю информацию о товарном запасе и работает в режиме реального времени.
 Т.е. вы видите и оцениваете текущую ситуацию на складе и можете быстро выявлять факторы повышенного риска, например, кража, повреждение товара и т.п. Вы можете быстрее оценивать продуктивность работы вашего персонала, и знать точно о времени выполнения той или иной операции, и, как следствие, какие процессы складской логистики у вас «проседают» и требуют доработок.
Т.е. вы видите и оцениваете текущую ситуацию на складе и можете быстро выявлять факторы повышенного риска, например, кража, повреждение товара и т.п. Вы можете быстрее оценивать продуктивность работы вашего персонала, и знать точно о времени выполнения той или иной операции, и, как следствие, какие процессы складской логистики у вас «проседают» и требуют доработок. Повышение скорости выполнения заказов
Текущая высококонкурентная среда требует от поставщиков сокращения времени выполнения заказа до дня или даже нескольких часов, и это уже становится нормой в работе торгового предприятия. Система управления складом будет тем инструментом, который позволит усовершенствовать процессы и вывести доставку заказов на новый уровень. Ваша команда, работающая под управлением WMS-системы с применением мобильных терминалов или других устройств/систем, позволяющих автоматизировать выполнение ручных операций, сможет быстрее собирать и упаковывать заказы, что позволит значительно уменьшить время обработки и доставки товаров.

Снижение затрат на складскую обработку
Если сократить время выполнения складских операций, например, отбор, упаковку заказов или приемку, а также других процессов, то это неизбежно повлечет за собой снижение ваших затрат на складскую обработку товара. Это достаточно просто проверить. Можно рассчитать текущую стоимость обработки каждого заказа при работе без системы управления складом и сравнить с данными после завершения проекта внедрения. И тогда вы сможете увидеть, какая окупаемость будет достигнута.
Минимизация ошибок
Система управления складом и штрих-кодированная продукция существенно сокращают время на обработку товара и снижают риск возникновения ошибок. Под управлением WMS-системы сотрудники склада сканируют штрих-код товара во время выполнения всех складских процессов: отбора, упаковки, отгрузки, приемки и т.д. Система управления складом инициирует всю активность персонала, при неверных операциях, например, сканировании другого товара, предупреждает об ошибочном действии, автоматически ведет учет товара, в режиме реального времени передает данные в учетную систему.
 Такая организация работы склада не только позволяет значительно сократить ошибки, но и повысить степень удовлетворенности ваших заказчиков, снизить количество отрицательных отзывов.
Такая организация работы склада не только позволяет значительно сократить ошибки, но и повысить степень удовлетворенности ваших заказчиков, снизить количество отрицательных отзывов. Экономия времени
Система управления складом сокращает время выполнения складских операций, особенно это важно для сборки и доставки заказов. Инвентаризация товара также выполняется быстрее, без ошибок, в режиме реального времени, без остановки работы склада. Терминалы сбора данных, считывающие штрих-код с продукции и передающие данные в систему для склада в режиме on-line также сокращают время проведения инвентаризации. Чтобы узнать о дополнительных преимуществах работы склада под управлением WMS-системы, прочитайте эту статью
Несколько простых советов по внедрению системы штрихкодирования:
Для внедрения на складе системы штрихкодирования требуется больше усилий, чем просто наклеить этикетки со штрих-кодом на товар и начать использовать радио-терминалы. Также вам нужно организовать эффективную работу склада и оптимизировать все складские процессы.
Также вам нужно организовать эффективную работу склада и оптимизировать все складские процессы.
При планировании работы склада нужно обратить внимание на следующие моменты :
- Оптимизируйте размещение товаров на складе;
- Самые востребованные товары размещайте ближе к упаковочной зоне;
- Выделите наиболее доступные зоны для высоко оборачиваемых продуктов в пиковый сезон, во время распродаж;
- Штрих-коды располагайте в удобном для сканирования положении.
Функционал WMS-системы управления складом:
WMS-система управления складом применяется для автоматизации работы склада, что обеспечивает управление бизнес-процессами и контроль выполнения складских операций (приемка, перемещение, хранение, комплектация, отгрузка, и т.д.), Программа интегрируется с учетными программами предприятия, обеспечивает полную прозрачность данных в цепочке поставок всей компании.
WMS-система управления складом Logistics Vision Suite, представляемая «АНТ Технолоджис», обладает высокой эффективностью, широким функционалом, имеет неоспоримые конкурентные преимущества, выражаемые в быстрой адаптации под требования склада.
Адаптивность и широта настроек позволяет владельцу создать логистическую систему, решающие индивидуальные потребности для управления логистическим бизнесом. LVS подходит для крупных и средних компаний с интенсивными процессами товарооборота. Подробно→
Logistics Vision Suite управляет работой складов различной специализации: V7склад, Kerama-Marazzi, «МГЛ МЕТРО ГРУП ЛОГИСТИКС», STS Logistics, Smart Logistic Group, Логистическое Агентство 20А, HOFF, «Авеста Фармацевтика», «МИНИМАКС», Simple, «Группа Полипластик», Incity, «Алвиса», «Айсберри» и другие. Смотреть всех клиентов →
Рассмотрите систему управления складом Logistics Vision Suite как эффективное решение для оптимизации работы вашего склада. Отправьте запрос нашему специалисту [email protected]
Узнать, нужна ли WMS вашему бизнесу →
Приемка товара
Система WMS управляет работой склада по предварительно настроенным бизнес-процессам, соблюдение которых является обязательным условием при выполнении всех операций, в том числе при приемке товара. Процесс приемки товара может быть настроен под требования пользователей системы, но основная задача обеспечить приемку товара с минимальными ошибками, экономя при этом время при выполнении операции.
Процесс приемки товара может быть настроен под требования пользователей системы, но основная задача обеспечить приемку товара с минимальными ошибками, экономя при этом время при выполнении операции.
Учет товара
Система для склада ведет учет товара, предоставляет пользователям актуальную информацию о его количестве, позволяет минимизировать затаривание склада ненужными остатками. Экономия складского пространства и бесперебойная работа логистики склада достигается за счет оптимального распределения и хранения запасов.
Оптимизация процесса хранения
Программа для склада предоставляет пользователям возможность моделирования эффективных схем хранения различных товаров, учитывающих их характеристики, например, такие как, вес товара или его спрос (скорость оборачиваемости товарных запасов). Это позволяет организовать процесс хранения таким образом, что более востребованные или тяжелые товары будут располагаться ближе к зоне отгрузке или товар, отгружаемый вместе, будет храниться рядом друг с другом, за счет чего времени для его обработки потребуется меньше. Учет многочисленных факторов хранения обеспечивает эффективную работу складской логистики.
Учет многочисленных факторов хранения обеспечивает эффективную работу складской логистики.
Управление персоналом
Централизованное управление складом сокращается необходимость в содержании персонала в большом количестве. Оптимизация рабочего фонда становиться возможной, в том числе, за счет сокращения частоты инвентаризации товара. WMS программа позволяет производить инвентаризацию товара без вмешательства в повседневную работу склада. Сокращение расходов на оплату труда позволяет снизить текущие (операционные) расходы на содержание склада и повысить эффективность работы всего предприятия. Измерение ключевых показателей эффективности работы склада (KPI склада) повышает эффективность работы, позволяет измерять показатели эффективности, проверять выполнение и результативность работы, формировать форму отчетности, настраивать систему мотивации и нормы оплаты труда.
Документооборот
WMS-система управления складом способна автоматизировать все процессы, устраняя необходимость ведения бумажного документооборота, требующего значительных ресурсов. Пользователи могут иметь общий доступ к базе данных, обеспечить работников необходимой информацией для быстрой и качественной работы.
Пользователи могут иметь общий доступ к базе данных, обеспечить работников необходимой информацией для быстрой и качественной работы.
Комплектация и отгрузка
Программа управления складом обеспечивает качественную сборку заказов, это означает, что процесс сборки будет выполнен по складским стандартам, методам FIFO, FEFO, FPFO и LIFO. WMS С такой системой ваши заказы будут правильно собраны и доставлены по верному адресу в необходимое время.
Обслуживание клиентов
WMS-система управления складом повышает качество обслуживания клиентов за счет быстрой и безошибочной обработки заказов поклажедателей и своевременной доставки. Высокое качество обслуживания повышает конкурентоспособность компании, позволяет формировать лояльность текущих заказчиков и привлекать новых клиентов.
Управление складом и контроль
Для предприятий, которым необходимы расширенные возможности контроля, программа предлагает отслеживать товар по различным характеристикам: серийные номера, сроки годности, товарные коды и т. п. Вопросы по возвратам и условиям гарантии качества товара быстро решаются путем возможности отслеживания каналов поставок.
п. Вопросы по возвратам и условиям гарантии качества товара быстро решаются путем возможности отслеживания каналов поставок.
Отчетность
Лучшие системы управления складом (Warehouse Management Systems), в число которых входит Logistics Vision Suite, позволяют так же просто использовать базы данных, как и Microsoft SQL, что обеспечивает возможность формирования отчетов даже в стандартных версиях решений. Но WMS-системы обладают преимуществом, они позволяют менять способы представления данных. На основании имеющейся информации можно формировать различные отчеты:
- эффективность использования складских площадей;
- необходимость увеличения или сокращения складских площадей;
- работоспособность каждого работника склада;
- оптимизация количества персонала;
- анализ финансовых затрат на основании данных об объеме хранения и количества выполненных операций;
- и др.
Как выбрать WMS-систему управления складом:
На рынке представлены различные типы WMS-систем, есть простые коробочные решения, а есть сложные комплексные системы управления складом, подходящие для крупных складов. Система управления складом Logistics Vision Suite относится к классу комплексных информационных систем, с полным набором функций и возможностью значительной модификации комплекса выполняемых задач в соответствии со спецификой и потребностями логистики компании, выполнение требований контролирующих органов: интеграция с государственными системами цифровой маркировки и прослеживаемости товаров «Честный Знак», ЕГАИС, «Меркурий».
Система управления складом Logistics Vision Suite относится к классу комплексных информационных систем, с полным набором функций и возможностью значительной модификации комплекса выполняемых задач в соответствии со спецификой и потребностями логистики компании, выполнение требований контролирующих органов: интеграция с государственными системами цифровой маркировки и прослеживаемости товаров «Честный Знак», ЕГАИС, «Меркурий».
Чтобы выбрать систему для управления складом необходимо учесть ряд факторов, некоторые из которых мы рассмотрим:
- Функциональность: представленные на рынке решения могут выполнять разные функции, так как могут быть ориентированы на разные отрасли. В каком функционале нуждается ваш бизнес, чтобы максимально удовлетворить ваши задачи, потребности ваших клиентов, контролирующих органов и акционеров компании? Выберите ту систему управления складом, которая обладает гибким функционалом и возможностью сильного масштабирования для поддержания всех требований развивающегося логистического бизнеса.
- Размер склада: крупным складам необходимы системы управления с более развитым функционалом, чем небольшим складским хозяйствам. Это объясняется более высокой сложностью выполняемых операций и большим объемом технологических процессов крупного склада. Чем крупнее склад, те сложнее вычислить стоимость одной транзакции, поэтому в этом случае, необходима организация детального отслеживания каждой складской операции.
- Потребности клиента: прежде чем начать внедрение определите необходимую для вас функциональность, выберете то программное обеспечение, которое сможет предоставить вам и вашим клиентам необходимый уровень сервиса. Например: у вас интернет-магазин и вам необходимо организовать учет товара в режиме реального времени или вам необходимо предоставить клиентам возможность отслеживания их заказов …
- WMS Цена: стоимость внедрения зависит от сложности проекта, объема работ и поставщика программного обеспечения.
 Выбирайте систему, ориентируясь на ее функционал, стоимость программы и услуг внедрения. Остановитесь на решении, цена которого будет оптимальной для вашего бизнеса. Как правило, базовая версия не имеет широкого функционала, способного покрыть все задачи логистики предприятия. Если у вас развитое предприятие с широким спектром задач, то правильным действием станет выбор программы, обладающей гибким адаптивным функционалом, реализация которой возможна за оптимальный для вас бюджет, например, такой, как WMS-система Logistics Vision Suite. Выбирая поставщика решения, думайте не только о текущих задачах склада, но и учитывайте долгосрочные потребности вашего склада, которые могут быть реализованы.
Выбирайте систему, ориентируясь на ее функционал, стоимость программы и услуг внедрения. Остановитесь на решении, цена которого будет оптимальной для вашего бизнеса. Как правило, базовая версия не имеет широкого функционала, способного покрыть все задачи логистики предприятия. Если у вас развитое предприятие с широким спектром задач, то правильным действием станет выбор программы, обладающей гибким адаптивным функционалом, реализация которой возможна за оптимальный для вас бюджет, например, такой, как WMS-система Logistics Vision Suite. Выбирая поставщика решения, думайте не только о текущих задачах склада, но и учитывайте долгосрочные потребности вашего склада, которые могут быть реализованы. Полезная информация
История успеха
Склад «Метро Груп Логистикс» работает под управлением WMS Logistics Vision Suite & Vocollect Voice
Новости
Все новости
Новости партнеров
Все новости партнеров
Ваш консультант:
Андрей Хвостиков
+7 (495) 785-72-28
Скачать буклет
Наши клиенты
Награды и достижения
Условия поставки FCA (Free Carrier) Инкотермс 2010 (актуально на 2017)
Содержание статьи:
- Что означает FCA: расшифровка
- Дополнительная терминология для FCA
- Базис и условия поставки FCA
- Распределение рисков и обязанностей
- Обязанности и риски продавца (поставщика)
- Обязанности и риски покупателя
- Переход права собственности и рисков
- Кто оформляет CMR?
- Что такое франко-перевозчик?
- Договор поставки на условиях FCA
- Что такое цена на условиях FCA?
Перейти на список всех условий Инкотермс
В сфере международной торговли действуют Правила Инкотермс в редакции 2010 года – правила исполнения обязательств сторонами договора. До 1 января 2011 года при составлении соглашения о купле-продаже участники процесса ВЭД руководствовались Правилами Инкотермс 2000 года. В новой редакции появились два новых понятия: DAT и DAP, которые заменили практиковавшиеся до 2011 года термины DAF, DES, DEQ и DDU. Следовательно, в Инкотермс 2010 стало меньше правил: 11 вместо 13. Это – EXW, FCA, CPT, CIP, DAT, DAP, DDP, применяющиеся независимо от вида транспорта для перевозки, и FAS, FOB, CFR и CIF применительно к морским перевозкам и транспортировке грузов на внутреннем водном транспорте.
До 1 января 2011 года при составлении соглашения о купле-продаже участники процесса ВЭД руководствовались Правилами Инкотермс 2000 года. В новой редакции появились два новых понятия: DAT и DAP, которые заменили практиковавшиеся до 2011 года термины DAF, DES, DEQ и DDU. Следовательно, в Инкотермс 2010 стало меньше правил: 11 вместо 13. Это – EXW, FCA, CPT, CIP, DAT, DAP, DDP, применяющиеся независимо от вида транспорта для перевозки, и FAS, FOB, CFR и CIF применительно к морским перевозкам и транспортировке грузов на внутреннем водном транспорте.
В данной статье мы рассмотрим термин FCA – Франко перевозчик.
Что означает FCA: расшифровка
Термин FCA используется при перевозке и расшифровывается как Free Carrier. Данное словосочетание дословно можно перевезти как «бесплатный» или «свободный» «перевозчик». При составлении договора применяется словосочетание «Франко перевозчик» (… название места). Если выразить простыми словами, термин означает, что обязательства продавца по отношению к товару сохраняются только до передачи им товара перевозчику, выбранному покупателем. Свобода в выборе покупателем логистической компании ничем не ограничена.
Свобода в выборе покупателем логистической компании ничем не ограничена.
Франко – это место, где ответственность за сохранность и транспортировку товара полностью перекладывается на плечи покупателя.
Под словом «Перевозчик» можно понимать лицо, которое согласно договору поставки продукции обеспечит транспортировку груза на определенном контрактом виде транспортного средства или его комбинации.
В условиях и порядке поставки товара указывается, что «поставка товара по контракту осуществляется на условиях FCA – Free carrier/Франко перевозчик – «Инкотермс 2010». Также указывается пункт передачи товара, например, ООО «ЧИСТО» при экспорте моющих средств для кофемашин в Китай могло бы обозначить: «FCA д. 31, ул. Бестужева, г. Владивосток, Приморский край, Российская Федерация, Инкотермс 2010».
Читайте также:
Все условия Инкотермс в удобной таблице
Дополнительная терминология для FCA
Обозначенное в контракте место поставки разграничивает обязательства продавца и покупателя по погрузке и разгрузке товара. Так, при поставке на территории, принадлежащей поставщику, ответственность за погрузочно-разгрузочные работы ложится на продавца, если в ином месте, то на покупателя. Разграничение обязанностей происходит с использованием дополнительных терминов. Так, когда нужно перевезти груз, объем которого полностью занимает все пространство вагона, машины, баржи, иного транспортного средства, то в договоре указывается:
Так, при поставке на территории, принадлежащей поставщику, ответственность за погрузочно-разгрузочные работы ложится на продавца, если в ином месте, то на покупателя. Разграничение обязанностей происходит с использованием дополнительных терминов. Так, когда нужно перевезти груз, объем которого полностью занимает все пространство вагона, машины, баржи, иного транспортного средства, то в договоре указывается:
- FOT (free on truck) (при перевозке авто).
- FIW (free in wagon) (ж/д перевозка).
- FIB (free into barge) (перевозка на барже).
Когда требуется консолидация груза, то можно согласовать с продавцом организацию доставки товара до терминала, склада, порта, который указывается продавцом. И тогда применяется следующая терминология:
- FT (free terminal) (терминал).
- FOR (free on rail) (станция отправления).
- FFB (free ferry berth) (паромный причал).
Пожалуйста, помогите сделать эту статью лучше.
Ответьте всего на 3 вопроса.
Базис и условия поставки FCA
Базисные условия FCA по Инкотермс 2010 создают существенные условия покупателю для возможности выбора транспортного средства для доставки груза, построения логистической цепочки.
Перевозчиком может стать транспортная компания или любое доверенное лицо покупателя, с кем заключен контракт на оказание логистических услуг.
Покупатель может выбрать мультимодальную доставку, автомобильную, ж/д, на воздушном судне, поездом и т.д.
Если отгрузка происходит непосредственно на складе продавца, то последний несет все расходы по погрузке. Когда в качестве франко-места определены терминал или иное место, не принадлежащее на праве собственности или аренды поставщику, то расходы на погрузку должен оплатить покупатель.
В обязанность продавца вменена очистка груза от экспортных пошлин: условия FCA предполагают сдачу товара с приложением подтверждающего документа. После передачи груза ответственность за товар несет покупатель.
После передачи груза ответственность за товар несет покупатель.
Таможенные расходы (на импорт) в стране получения также осуществляет покупатель.
Распределение рисков и обязанностей
Обязанности продавца и покупателя по правилам FCA четко разграничены.
Обязанности и риски продавца (поставщика)
В обязанность продавца вменено предоставление покупателю товара, счета-фактуры, иной документации, наличие которых обговорено в контракте.
Получить лицензию для экспорта продукции, иное свидетельство, выполнить таможенные формальности при вывозе, все это – задачи продавца.
Отсутствуют обязательства по страхованию и фрахту груза. Продавцу необходимо только предоставить товар компании-перевозчику в указанном в договоре месте, в установленные сроки и время. Поставку можно считать выполненной, если соблюден ряд условий:
- Товар загружен в транспорт компании-перевозчика в помещении, принадлежащем продавцу.

- Товар в транспортном средстве продавца готов к отгрузке в транспорт перевозчика, если франко-место расположено за территорией, собственником которой является продавец.
Продавец несет расходы, связанные с товаром до его поставки покупателю, а также оплачивает экспортные пошлины, налоги, иные сборы.
О поставке товара продавец должен известить покупателя должным образом.
Доказательствами поставки являются транспортные документы, в том числе в электронном виде, если стороны договора пришли к соглашению об использовании средств электронной связи.
Расходы на упаковку ложатся на продавца. Она должна быть надлежаще маркирована.
Продавец может оказать содействие покупателю в получении иных документов, которые нужны для импорта товара. Но только за счет последнего.
Обязанности и риски покупателя
Основная обязанность покупателя – в оплате полной стоимости товара согласно договору купли-продажи.
Кроме этого, будут следующие денежные расходы:
- На покупку импортной лицензии, свидетельства, возмещение затрат на таможенные формальности при импорте.
- Транспортировку груза от франко-места до места назначения.
- Расходы, связанные с товаром, после его поставки на франко-место.
- На транзитную перевозку через третьи государства.
- На предпогрузочный осмотр груза.
- Возмещение расходов продавца, если он помогал оформить договор перевозки.
Покупатель обязан принять поставку товара, если она выполнена согласно договору.
Покупатель извещает должным образом продавца о наименовании перевозчика, способе транспортировки, дате и сроках поставки товара для передачи перевозчику.
Кроме этого, покупателю за 10 дней до поставки товара нужно будет предоставить перевозчику следующие данные:
- Наименование товара, его объем;
- Полное и краткое наименование компании-грузоотправителя;
- Дата и время загрузки, точный адрес места загрузки, например, склад продавца;
- Полное наименование компании-грузополучателя и краткое;
- Точный адрес грузополучателя.
 При отсутствии номера квартиры об этом должна быть соответствующая пометка;
При отсутствии номера квартиры об этом должна быть соответствующая пометка; - Коды грузополучателя;
- Коды железнодорожных станций при доставке ж/д путем;
- Иные сведения, которые позволят перевозчику уложиться по срокам доставки.
Переход права собственности и рисков
Моментом перехода права собственности и исполнения обязательств продавцом считается завершение загрузки товара в транспортное средство перевозчика, если франко-место – склад поставщика, например. В ином случае права собственности на товар переходят покупателю при доставке до места загрузки на транспорт перевозчика, которое не принадлежит продавцу.
До этого момента все риски за товар несет продавец, после – покупатель.
В случае, когда покупатель не смог вовремя вывезти товар, то и переход рисков осуществляется с даты, когда он должен был организовать перевозку груза.
Кто оформляет CMR?
При перевозке товара по Европе нужно оформлять международную накладную CMR. В ней содержится информация о продавце, покупателе груза, виде товара, его весе и объеме.
В ней содержится информация о продавце, покупателе груза, виде товара, его весе и объеме.
Накладная заполняется отправителем груза, то есть продавцом. Инструкции и указания должна предоставить компания-перевозчик. За достоверность заполнения CRM продавец и перевозчик несут солидарную ответственность.
Что такое франко-перевозчик?
Термин «франко-перевозчик» в толковании Инкотермс 2010 означает доставку продавцом товара, прошедшего таможенную очистку, до франко-места и его передачу перевозчику, нанятому покупателем. В контракте данное понятие употребляется с указанием точного адреса загрузки товара.
Допустим, завод-производитель ООО «Элитный паркет» заключил контракт с покупателем из США. В условиях поставки место «франко-перевозчика» указывается так: «Пунктом передачи является склад ООО «Элитный паркет» по адресу: д. 10, стр. 3, ул. Сыромятническая Ниж., Москва, Российская Федерация», если это – территория продавца. Но можно указать и терминал в Домодедово, если покупатель определил по условиям fca эту территорию для передачи груза перевозчику. Тогда нужно оформить следующим образом: «Пунктом передачи является грузовой терминал аэропорта Домодедово по адресу: с. 7/1, Домодедово аэропорт, Московская обл., Российская Федерация».
Но можно указать и терминал в Домодедово, если покупатель определил по условиям fca эту территорию для передачи груза перевозчику. Тогда нужно оформить следующим образом: «Пунктом передачи является грузовой терминал аэропорта Домодедово по адресу: с. 7/1, Домодедово аэропорт, Московская обл., Российская Федерация».
Пожалуйста, помогите сделать эту статью лучше.
Ответьте всего на 3 вопроса.
Договор поставки на условиях FCA
Предлагаем вашему вниманию готовый вариант международного договора поставки по условиям FCA. Образец составлен с учетом основных положений терминологии Инкотермс 2010 и в полной мере содержит обязательства и покупателя, и продавца. Если вам нужны консультации по представленному документу, мы готовы вам помочь. Образец контракта можно скачать без регистрации и бесплатно.
Цена на условиях FCA
При подписании двустороннего договора на поставку товара в цену на условиях FCA продавец включает следующие расходы:
- Стоимость товара по факту;
- Расходы на экспортные пошлины на таможне;
- Расходы на доставку груза до места передачи перевозчику.

Когда заключается контракт международной купли-продажи товара, обе стороны внешнеэкономической деятельности должны как можно четче и детальнее прописать условия поставки. Указание свойств товара, обозначение типа транспортного средства, объема груза и другие данные позволят избежать задержек на таможне и дополнительных расходов на экспортные и импортные пошлины и сборы.
Принцип классификации судов РКО (выдержка из правил)
21.06.2017
Принцип классификации судов РКО (выдержка из правил)
ПРИНЦИПЫ КЛАССИФИКАЦИИ СУДОВ РОССИЙСКОГО КЛАССИФИКАЦИОННОГО ОБЩЕСТВА
7.1. Класс судна определяется совокупностью условных символов, присваиваемой судну при его классификации и характеризующей конструктивные особенности судна и условия его эксплуатации в соответствии с правилами исходя из требований безопасности.
7. 2. Классификация судов осуществляется в соответствии с классификацией водных бассейнов.
2. Классификация судов осуществляется в соответствии с классификацией водных бассейнов.
7.3. Внутренние водные бассейны, включая участки с морским режимом судоходства, классифицируются по разрядам «Л», «Р», «О» и «М» в зависимости от их ветро–волнового режима исходя из следующих условий:
1) в бассейнах разрядов «Л», «Р» и «О» волны 1 %-ной обеспеченности высотой соответственно 0,6, 1,2 и 2,0 м имеют суммарную повторяемость (обеспеченность) не более 4% навигационного времени;
2) в бассейнах разряда «М» волны 3%-ной обеспеченности высотой 3,0 м имеют суммарную повторяемость (обеспеченность) не более 4% навигационного времени.
Участки с морским режимом судоходства начинаются от границы внутренних водных путей. В этих участках могут эксплуатироваться суда всех типов в соответствии с правилами и классом судна. Перечни внутренних водных бассейнов России в зависимости от их разряда, а также морские районы, в которых может осуществляться эксплуатация судов смешанного (река – море) плавания, и условия эксплуатации судов устанавливаются правилами. Морские районы классифицируются по разрядам «О-ПР», «М-ПР» и «М-СП» в зависимости от их ветро-волнового режима и обеспеченности местами убежища.
Морские районы классифицируются по разрядам «О-ПР», «М-ПР» и «М-СП» в зависимости от их ветро-волнового режима и обеспеченности местами убежища.
7.4. Основными символами в формуле класса судов внутреннего плавания являются буквы «Л», «Р», «О» и «М», определяющие конструктивные особенности судна и разряд водного бассейна, в котором оно может эксплуатироваться.
Основными символами в формуле класса судов смешанного (река – море) плавания являются буквенные сочетания «О-ПР», «М-ПР» и «М-СП», определяющие конструктивные особенности судна и условия его эксплуатации в морских районах. Характеристики нормативных высот волн применительно к основному символу класса судна приведены в приложении ¹ 2 к настоящему Положению.
7.5. В зависимости от конструктивных особенностей судна основной символ класса в формуле класса дополняется следующими символами:
1) для судов, построенных под техническим наблюдением Речного Регистра или другой признанной Речным Регистром классификационной организации, — символом ‡, который ставится перед основным символом, например, «‡О»;
2) непосредственно после основного символа класса вносится допускаемая при эксплуатации высота волны в метрах с точностью до первого знака после запятой, например, «‡О1,5».
Для высокоскоростных судов: глиссеров, судов на подводных крыльях (СПК), судов на воздушной подушке (СВП), а также экранопланов ограничения по высоте волны записываются в виде дроби, в числителе которой указывается высота волны при движении судна в водоизмещающем состоянии, а в знаменателе ‑ в эксплуатационном режиме. После дроби указывается тип судна по принципу движения, например, «‡Р1,2/0,8 глиссер», «‡О2,0/1,2 СПК», «‡О2,0/1,5 СВП», «‡Р1,2/0,4 экраноплан»;
3) для судов, имеющих специальные ледовые усиления, после значения высоты волны записываются заключенные в скобки слово «лед» и толщина мелкобитого зимнего льда в сантиметрах, установленная Речным Регистром при согласовании проекта судна, например, «‡О (лед 20)». В формулу класса ледоколов вносится слово «ледокол»;
4) для судов, оборудованных средствами автоматизации в соответствии с правилами, после всех символов, указанных в подпунктах 1 – 3 данного пункта, вносится буква «А», например, «‡О2,0 (лед 20) А»;
5) если судно или его отдельные элементы не в полной мере соответствуют правилам, не проверены практикой эксплуатации, но признаны Речным Регистром годными к эксплуатации как экспериментальные с целью их изучения и проверки, в формулу класса перед символом «‡» вносится символ «Э», например, «Э‡О2,0 (лед 20) А».
При удовлетворительных результатах испытаний, эксплуатации и освидетельствований судна с экспериментальным классом символ «Э» из формулы класса может быть исключен.
7.6. Речной Регистр может исключить или изменить в формуле класса тот или иной символ при изменении или нарушении условий, послуживших основанием введения в формулу класса данного символа.
7.7. Речной Регистр присваивает класс судну при первоначальном освидетельствовании, подтверждает, возобновляет или восстанавливает его при других видах освидетельствований. Присвоение, возобновление или восстановление класса судну удостоверяется выдаваемым на судно классификационным свидетельством.
7.8. Класс судна, эксплуатируемого постоянно в бассейне данного разряда, должен быть не ниже разряда этого бассейна.
7.9. Судно внутреннего плавания, имеющее годное техническое состояние, может быть признано пригодным к эпизо-
дическому плаванию (нерегулярной эксплуатации) в бассейне более высокого разряда при условии выполнения дополнительных требований по конструкции, надводному борту, оборудованию, снабжению, а также ограничений по району плавания, ветро–волновому режиму, сезонности, ледовым условиям и т. п.
п.
7.10. Речной Регистр по заявке судовладельца проводит переклассификацию судов в случае необходимости изменения основного символа класса в формуле класса или типа и назначения судна.
7.11. Работы по подготовке судна к переклассификации с повышением класса и/или в связи с изменением типа и назначения судна должны проводиться в соответствии с технической документацией, согласованной с Речным Регистром, и под его техническим наблюдением. Расчеты и проверки должны выполняться в соответствии с правилами, действующими на момент разработки технической документации по переклассификации, и должны быть ориентированы на новые условия эксплуатации в связи с изменением внешних нагрузок, технических характеристик (осадка, водоизмещение, высота надводного борта), рода перевозимого груза и т. п.
ПРИЛОЖЕНИЕ ¹ 1
УКАЗАНИЯ ПО ОПРЕДЕЛЕНИЮ ВМЕСТИМОСТИ
Под вместимостью понимается валовая вместимость судна. Валовая вместимость судов внутреннего плавания GT в регистровых тоннах определяется по формуле:
Валовая вместимость судов внутреннего плавания GT в регистровых тоннах определяется по формуле:
,
где V — валовая вместимость, м3, определяемая путем обмера всех помещений судна или подсчитываемая по формуле:
,
где L и B — длина и ширина судна по конструктивной ватерлинии, м;
H — высота борта, м; T — осадка судна по конструктивную ватерлинию, м; d — коэффициент полноты водоизмещения; a —коэффициент полноты конструктивной ватерлинии; l, b, h — соответственно средние длина, ширина и высота надстроек или рубок, м. В валовую вместимость не включаются объемы рулевой рубки, камбузов, туалетов, всех световых люков и сходных мелких рубок. Валовая вместимость судов смешанного (река – море) плавания определяется в соответствии с правилами обмера судов, содержащимися в Приложении ¹ 1 к Международной конвенции по обмеру судов 1969 года.
ПРИЛОЖЕНИЕ ¹ 2
ХАРАКТЕРИСТИКИ НОРМАТИВНЫХ ВЫСОТ ВОЛН ПРИМЕНИТЕЛЬНО К ОСНОВНОМУ СИМВОЛУ КЛАССА СУДНА
Основной символ класса «Л» «Р» «О» «М» «О-ПР» «М-ПР» «М-СП»
Нормативная высота волны, м 0,6 1,2 2,0 3,0 2,0 2,5 3,5
Обеспеченность высот волн, % 1 1 1 3 3 3 3
Математика | Бесплатный полнотекстовый | Генерация распределенного ключа на основе R-LWE и дешифрование порога
1. Введение
Появление компьютера в XX веке вызвало бурный рост криптографии, безопасность которой способствовала огромному развитию подключенного общества (например, недавнее криптографические усилия по облегчению реализации модели «умного города» [1]). Точно так же развитие квантовых вычислений и, в частности, алгоритма Шора [2], который делает криптографию, основанную на задачах дискретного логарифмирования и простого факторинга, практически бесполезной против квантового противника, породило новые типы криптографии.
Существует два основных типа криптографии, которые были разработаны для защиты от атак квантовых компьютеров: квантовая и постквантовая криптография. Квантовая криптография опирается на квантовые алгоритмы, которые не могут быть взломаны квантовыми противниками, в то время как постквантовая имеет дело с классическими (неквантовыми) алгоритмами, которые не могут быть взломаны квантовыми противниками. Мы сосредоточимся на постквантовой криптографии, учитывая, что широкое использование умеренно мощных квантовых компьютеров кажется недостижимым в краткосрочной перспективе. В этой области областью, в которой произошли последние достижения, является криптография на основе решетки, о чем свидетельствует тот факт, что в отчете о состоянии второго раунда процесса стандартизации постквантовой криптографии Национального института стандартов и технологий (NIST) [ 3] большинство финалистов третьего раунда представляют собой схемы на основе решетки. В схемах на основе решетки криптография, основанная на проблеме обучения с ошибками (LWE) и ее вариантах, особенно актуальна. Мы будем строить наши предложения вокруг проблемы кольцевого обучения с ошибками (R-LWE).
Мы будем строить наши предложения вокруг проблемы кольцевого обучения с ошибками (R-LWE).
Существует множество применений постквантовой криптографии, но основное внимание мы уделяем электронному голосованию. Электронное голосование характеризуется значительным недоверием. Отсутствие доверия к другим объектам — это то, что изначально породило концепцию криптографии, поэтому дальнейшее продвижение в этом направлении — следующий логический шаг. Поэтому цель состоит в том, чтобы «распространить» это доверие, чтобы один-единственный коррумпированный игрок больше не мог нарушить протокол. Распределенная криптография — это идея распределения задач между несколькими игроками, так что только определенные их подмножества могут выполнять криптографический протокол. Интерес к распределенной криптографии и, в частности, к постквантовой распределенной криптографии можно увидеть в интересных недавних достижениях в этой области, таких как [4,5].
Добавление постквантовой и распределенной криптографии, наконец, приводит нас к нашей основной теме: генерация распределенного ключа на основе R-LWE и пороговое дешифрование.
1.1. State-of-the-Art
Несмотря на проявленный интерес и потенциальную полезность криптографии с пороговым шифрованием с открытым ключом на основе решетки, количество существующих предложений невелико, особенно предложений, посвященных проблеме R-LWE. Большинство существующих предложений вращаются вокруг проблемы LWE (см., например, [5, 6, 7, 8]), которая имеет потенциальную проблему роста ключей и шифротекстов с O (n2), а не с O (n), как вариант R-LWE (где n — размерность решетки), таким образом, с большей вероятностью потребуется большее количество операций и, следовательно, время вычислений. В мире порогового шифрования на основе R-LWE, насколько нам известно, есть только одно предложение, приведенное в [9].], которая основана на гомоморфных свойствах представленной полностью гомоморфной схемы шифрования. Однако это предложение не включает протокол распределенной генерации ключей (поскольку для этого используется доверенная третья сторона (TTP)). Кроме того, насколько нам известно, ни одно из упомянутых предложений не дает реализации для действительного анализа времени вычислений, даже если реализация постквантовых протоколов является горячей темой, как показано в проекте Open Quantum Safe [10]. Кроме того, проект Open Quantum Safe также показывает нам, что, несмотря на недавние разработки, большинство приложений все еще находятся на стадии прототипа. Краткую информацию о текущем состоянии техники можно найти в таблице 1.
Кроме того, проект Open Quantum Safe также показывает нам, что, несмотря на недавние разработки, большинство приложений все еще находятся на стадии прототипа. Краткую информацию о текущем состоянии техники можно найти в таблице 1.
1.2. Вклады
В этой работе мы представляем оригинальные протоколы как распределенной генерации ключей, так и пороговой дешифровки, которые, насколько нам известно, являются первыми пороговыми протоколами на основе R-LWE, включая как дешифрование, так и генерацию ключей. Протоколы основаны на предложении LWE, представленном Бендлином и Дамгардом в [6], чьи идеи перенесены в настройку R-LWE. Кроме того, мы доказываем правильность и безопасность этих протоколов, мы даем набор параметров, для которых наши протоколы имеют более 100 бит безопасности, и мы даем грубую реализацию протоколов на C для анализа их производительности.
1.3. Структура
В разделе 2 мы дадим предварительные сведения, необходимые для работы в области криптографических примитивов, распределенной криптографии и кольцевого обучения с ошибками. В разделе 3 мы представляем протоколы, которые являются основным вкладом в эту работу, в то время как в разделе 4 мы докажем их правильность, а в разделе 5 мы докажем их безопасность. Раздел 6 будет посвящен анализу реализации протоколов на C, и, наконец, в Разделе 7 мы дадим наши окончательные выводы и возможную дальнейшую работу. Для приложений в Приложении A мы приводим доказательства правильности и безопасности против злоумышленника, активно действующего в обоих протоколах, в Приложении B мы приводим доказательства для вспомогательных результатов, а в Приложении C мы даем ссылку на репозиторий, содержащий соответствующий код нашего протокола. выполнение.
В разделе 3 мы представляем протоколы, которые являются основным вкладом в эту работу, в то время как в разделе 4 мы докажем их правильность, а в разделе 5 мы докажем их безопасность. Раздел 6 будет посвящен анализу реализации протоколов на C, и, наконец, в Разделе 7 мы дадим наши окончательные выводы и возможную дальнейшую работу. Для приложений в Приложении A мы приводим доказательства правильности и безопасности против злоумышленника, активно действующего в обоих протоколах, в Приложении B мы приводим доказательства для вспомогательных результатов, а в Приложении C мы даем ссылку на репозиторий, содержащий соответствующий код нашего протокола. выполнение.
Большая часть введения взята из введения в магистерскую диссертацию [11] Феррана Олборха.
2. Предварительные
2.1. Обозначение
Элементы в R, Z или Zq будут обозначаться строчными буквами (a, b, …), а элементы в Rn, Zn или Zqn будут обозначаться жирными строчными буквами (a,b,…) . Мы будем рассматривать Zq с представителями в −q2,q2. Пусть X — случайная величина, X∼χ означает, что X следует распределению вероятностей χ, x⟵χ означает, что x выбирается из случайной величины, следующей за распределением χ, Y⟵χn означает, что Y является вектором таким, что каждая координата независимо выбирается из распределение χ и для любого множества J, j ← $J есть действие равномерного случайного выбора j из J. Мы также будем отождествлять любой многочлен степени n−1, f(x)=a0+a1x+…+an−1xn −1∈Zq[x] с вектором f=(a0,a1,…,an−1)∈Zqn. Говорят, что функция g пренебрежимо мала над n (g:=neg(n)), если ∀k∈Z>0,∃n0∈Z>0 такое, что ∀n≥n0,|g(n)|<1nk. Наконец, говорят, что функция f равна O(g(n)), если существуют M>0 и n0 такие, что |f(n)|≤M·g(n) для всех n>n0, а функция f является называется ω(g(n)), если для всех M>0 существует n0 такое, что |f(n)|>M·g(n) для всех n>n0.
Мы будем рассматривать Zq с представителями в −q2,q2. Пусть X — случайная величина, X∼χ означает, что X следует распределению вероятностей χ, x⟵χ означает, что x выбирается из случайной величины, следующей за распределением χ, Y⟵χn означает, что Y является вектором таким, что каждая координата независимо выбирается из распределение χ и для любого множества J, j ← $J есть действие равномерного случайного выбора j из J. Мы также будем отождествлять любой многочлен степени n−1, f(x)=a0+a1x+…+an−1xn −1∈Zq[x] с вектором f=(a0,a1,…,an−1)∈Zqn. Говорят, что функция g пренебрежимо мала над n (g:=neg(n)), если ∀k∈Z>0,∃n0∈Z>0 такое, что ∀n≥n0,|g(n)|<1nk. Наконец, говорят, что функция f равна O(g(n)), если существуют M>0 и n0 такие, что |f(n)|≤M·g(n) для всех n>n0, а функция f является называется ω(g(n)), если для всех M>0 существует n0 такое, что |f(n)|>M·g(n) для всех n>n0.
2.2. Криптографические примитивы
Мы начнем с описания некоторых криптографических примитивов, известных определений, протоколов или методов, используемых в криптографии, на основе которых мы будем строить нашу схему и протоколы шифрования. Во-первых, мы формально определим, что такое схема шифрования.
Во-первых, мы формально определим, что такое схема шифрования.
После того, как мы определили криптосистему, нам нужно доказать некоторые ее свойства, чтобы убедиться, что она полезна. Наиболее важными из этих свойств являются правильность и безопасность, и с этого момента мы сосредоточимся исключительно на шифровании с открытым ключом.
В отличие от правильности схемы шифрования, безопасность можно определить по-разному. Это связано с тем, что расшифровка всегда должна быть правильной (или всегда, за исключением незначительной вероятности), но безопасность зависит от свойств противника, от которого мы хотим нас защитить (доступная информация, вычислительная мощность), и того, что мы хотим гарантировать. (что злоумышленник не может знать, какое сообщение было зашифровано, или что он не может отличить, какое сообщение было зашифровано, из пула открытых текстов). В нашем случае нас интересует безопасность CPA.
Кроме того, безопасность может быть достигнута против различных типов противников в зависимости от того, какими возможностями они обладают. Мы сосредоточимся в основном на пассивных противниках (также известных как честные, но любопытные), которые могут видеть всю информацию, которую имеют испорченные игроки, но не могут заставить их отклониться от протокола, и активных противниках (также известных как злонамеренные), которые могут заставить игроки произвольно отклоняются от протокола. Еще одно важное различие, которое следует сделать, заключается в том, является ли это статическим противником, который выбирает подмножество игроков, которых он испортит, до запуска протокола; или динамический противник, который может изменить подмножество поврежденных игроков во время выполнения протокола. Наша модель безопасности будет направлена против статических противников.
Мы сосредоточимся в основном на пассивных противниках (также известных как честные, но любопытные), которые могут видеть всю информацию, которую имеют испорченные игроки, но не могут заставить их отклониться от протокола, и активных противниках (также известных как злонамеренные), которые могут заставить игроки произвольно отклоняются от протокола. Еще одно важное различие, которое следует сделать, заключается в том, является ли это статическим противником, который выбирает подмножество игроков, которых он испортит, до запуска протокола; или динамический противник, который может изменить подмножество поврежденных игроков во время выполнения протокола. Наша модель безопасности будет направлена против статических противников.
2.3. Распределенная криптография
Конкретная отрасль криптографии, которая нас интересует в этой работе, — это распределенная криптография.
Одной из первых схем обмена секретами и одной из наиболее используемых до сих пор из-за простоты вычислений и понимания является Shamir Secret Sharing. Мы будем активно использовать его на протяжении всей нашей работы.
Мы будем активно использовать его на протяжении всей нашей работы.
Удобство этой схемы разделения секрета заключается в двух основных свойствах: восстановление секрета осуществляется с помощью интерполяции Лагранжа (которую легко вычислить) и доли являются линейными, что означает, что линейная комбинация долей является долей линейной комбинации секретов. Оба этих свойства будут использоваться в нашей работе.
Другими распределенными криптографическими инструментами, которые мы будем использовать, являются методы псевдослучайного совместного использования секрета (PRSS) и неинтерактивного верифицируемого совместного использования секрета (NIVSS). Эти инструменты будут иметь решающее значение в нашем предложении, поскольку безопасность наших протоколов основана на возможности маскировать соответствующую информацию шумом таким образом, чтобы злоумышленник не мог ее получить. Для генерации этого шума мы будем использовать эти два протокола.
Наконец, поскольку мы будем использовать распределенные методы, необходимо убедиться, что порядок, в котором различные игроки отправляют информацию, не ставит под угрозу безопасность схемы. Вообще говоря, последний игрок, который отправит информацию, будет иметь преимущество по сравнению с первым из-за знания большего количества информации при принятии решения. Для решения этой проблемы стандартно использовать схемы обязательств.
Вообще говоря, последний игрок, который отправит информацию, будет иметь преимущество по сравнению с первым из-за знания большего количества информации при принятии решения. Для решения этой проблемы стандартно использовать схемы обязательств.
2.4. Кольцевое обучение с ошибками
Задача обучения с ошибками (LWE) была введена Регевом в 2005 г. в предыдущей версии [15] как обобщение задачи обучения по четности и дала основанный на ней криптографический протокол и сокращение его безопасность к проблеме жесткой решетки (проблема кратчайшего вектора GAP (GAPSVP)).
Однако у криптосистем, основанных на проблеме LWE, есть несколько проблем. Например, многие из них должны шифроваться побитно, и, что более важно, требуемые открытые ключи очень дорого хранить, поскольку они обычно представляют собой (большие) матрицы элементов в Zq. Соединяя эти два фактора вместе, мы получаем, что для шифрования небольших объемов информации обычно требуется много места для хранения.
Для решения этих проблем вариант кольцевого обучения с ошибками был представлен Любаевским, Пейкертом и Регевом в [16]. По сути, это частный случай LWE, но в кольцах полиномов над конечными кольцами. Задача над кольцом многочленов Rq=Zq[x]/〈f〉, где f — унитарный многочлен от Zq[x].
Для данного элемента a(x)∈Rq можно увидеть главный идеал, порожденный a(x)
как идеальную решетку в Zqn, которую мы будем обозначать как L(a). Это соответствие легко увидеть в случае f(x)=xn+1 (конкретное Rq мы будем использовать с учетом его конкретных свойств) благодаря тому, что вектор коэффициентов произведения полиномов в Rq можно найти через антициклическая матрица выглядит следующим образом:
где a=(a1,…,an) и b=(b1,…,bn) — коэффициенты при a(x) и b(x) соответственно.
После этого мы можем, наконец, определить проблему кольцевого обучения с ошибками, на которой основана большая часть криптографии на основе решетки.
Таким образом, выборка распределения R-LWE представляет собой точку идеальной решетки, смещенную на запас, заданный распределением χ (которое обычно берется таким образом, чтобы ошибка была небольшой). Поэтому задачу поиска R-LWE можно рассматривать как нахождение точки в идеальной решетке L(a) (помните, что вектор a однозначно определяет идеальную решетку через свою антициклическую матрицу), «близкой» к выборке, и решение R -LWE можно рассматривать как заданную идеальную решетку L(a), решить, все ли заданные точки «близки» к L(a) или распределены равномерно.
При реализации LWE или R-LWE мы будем использовать определенный тип распределения вероятностей по Zq, называемый дискретными гауссианами, учитывая их хорошие свойства и простоту выборки значений из них. Существует несколько различных определений дискретных гауссианов, но в нашей реализации мы будем использовать следующее, так как его гораздо проще выбрать.
Обратите внимание, что если Y ~ Ψσ, то Y = X (mod1), где X ~ N (0, σ), где уменьшение по модулю 1 берет только десятичную часть любого действительного числа.
Заметим, что если Z∼Ψ¯σ, то Z=⌊qY⌉(modq), где Y∼Ψσ.
3. Схема шифрования и протоколы
Проведя все необходимые предварительные приготовления, мы можем, наконец, представить нашу схему шифрования, протокол порогового дешифрования и протокол генерации распределенного ключа, правильность которых мы докажем в разделе 4, безопасность – в разделе 5, проанализируем их реализации в Разделе 6 и дать некоторые последние мысли и возможные будущие работы в Разделе 7.
Мы будем использовать версию схемы шифрования LPR, представленную в [16].
Схема шифрования 1. Пусть q,n,u∈Z>0, где u — количество игроков, а χ — распределение по Rq. Схема шифрования S=(M,C,K,E,D) и генерация ключа, которые мы будем использовать, следующие:
M={0,1}n⊆Zqn≅Rq. Мы будем рассматривать каждый m∈M как элемент в Rq, где m — его вектор коэффициентов.
C⊆Rq×Rq.
Это общедоступная схема шифрования, у нас есть Ks⊆Rq и Kp⊆Rq×Rq.

- –
Для любой пары ключей (pk,s)∈Kp×Ks мы будем иметь s⟵∑i=1uχ (что означает сумму u отсчетов χ) и pk=(aE,bE) =(aE,aE·s+e), где aE ←$Rq и e⟵∑i=1uχ.
E={Epk:pk=(aE,bE)∈Kp} такое, что для заданного сообщения m∈M:
где(u,v)=(aE·rE+eu,bE·rE+ ev+m·⌊q2⌋) с rE,eu,ev⟵χ.
D={Ds:s∈Ks} такое, что для заданного зашифрованного текста (u,v)∈C:
, где мы восстановим каждый бит m, округлив каждый коэффициент
до 0 или ⌊q2⌋(modq) а затем сопоставляем 0 с 0 и ⌊q2⌋ с 1.
Теперь мы определим протокол порогового дешифрования на основе этой схемы шифрования и протокол генерации распределенного ключа для совместной работы с ним. Для ясности мы используем TTP для генерации ключей в протоколе шифрования, однако мы ищем полностью распределенную схему, поэтому мы также определяем протокол распределенной генерации ключей, чтобы заменить TTP в протоколе порогового дешифрования. .
.
См. Таблицу 2.
Для протокола генерации ключей предполагается, что на начальных этапах взаимодействия используется схема фиксации, когда вся выборка выполнена и отправлена.
См. Таблицу 3 для более подробного ознакомления с этапами необходимого взаимодействия. Заметим, что субиндексами мы будем обозначать аддитивные вклады, а супериндексами — доли Шамира.
4. Корректность
Имея на руках все предварительные данные и определив оба протокола, мы можем приступить к доказательству их правильности. Мы приведем доказательство для случая пассивного противника на этапе генерации ключа и активного (или пассивного) противника на этапе дешифрования, так как это будет случай, который будет использоваться в нашей реализации, причины такого решения будут объяснены в Раздел 6.1. Доказательство для случая, когда во время протокола генерации ключей присутствует активный противник, будет в Приложении A.1.
В случае, когда мы комбинируем оба протокола, что означает, что мы заменяем TTP в протоколе 1 протоколом 2, выходные данные этого протокола и TTP одинаково генерируются для случая пассивного противника на этапе генерации ключа, как он не может заставить любого игрока отклониться от протокола. Следовательно, мы можем напрямую применить теорему 1. Более того, та же теорема и доказательство верны против пассивного противника, развращающего до t=u−1 игроков, только с учетом того, что у нас будут все расшифровки правильными, поскольку пассивный противник не может сделать никаких ошибок. Игрок отклоняется от протокола.
Следовательно, мы можем напрямую применить теорему 1. Более того, та же теорема и доказательство верны против пассивного противника, развращающего до t=u−1 игроков, только с учетом того, что у нас будут все расшифровки правильными, поскольку пассивный противник не может сделать никаких ошибок. Игрок отклоняется от протокола.
5. Безопасность
Мы разделим доказательства безопасности протоколов на несколько теорем, чтобы упростить доказательства. Сначала мы докажем CPA-безопасность Схемы шифрования 1 как однопользовательской схемы, а затем докажем, что при распространении протоколов не происходит утечки информации. Наконец, мы добавим все, чтобы доказать безопасность CPA обоих протоколов, используемых вместе.
5.1. Безопасность схемы шифрования
Мы разделим доказательство безопасности схемы шифрования 1 на три отдельные части: сведение безопасности схемы шифрования к проблеме принятия решений R-LWE, сведение проблемы R-LWE с распределением Ψ¯n к проблема R-LWE с усеченным дискретным гауссовым и, наконец, сведение проблемы R-LWE с принятием решений к дискретной гауссовской выборке по K (K-DGS) с полем K, таким что R является его кольцом целых чисел, хорошо известная проблема решетки предполагается трудноразрешимой. Мы проведем это расщепление, потому что первая редукция будет для любого распределения χ, а вторая редукция будет конкретно для распределения Ψ¯n. Первая редукция следует идеям редукции схемы шифрования Регева к LWE, приведенным в [15]. Подробное доказательство см. в Приложении B.
Мы проведем это расщепление, потому что первая редукция будет для любого распределения χ, а вторая редукция будет конкретно для распределения Ψ¯n. Первая редукция следует идеям редукции схемы шифрования Регева к LWE, приведенным в [15]. Подробное доказательство см. в Приложении B.
Обратите внимание, что снижение касается семантической безопасности схемы, а не безопасности CPA. Однако хорошо известно, что в шифровании с открытым ключом оба понятия эквивалентны (см., например, теорему 11.1 в [12]).
Во-вторых, мы хотим иметь возможность гарантировать, что, если мы знаем, как решить экземпляр задачи решения R-LWE с усеченной дискретной гауссианой, мы можем решить экземпляр задачи решения R-LWE с распределением Ψ¯n . Это ясно, поэтому, учитывая пример задачи R-LWE решения с распределением Ψ¯n, можно рассматривать его как пример с усеченным дискретным гауссовым распределением, за исключением незначительного количества раз. Следовательно, преимущество противника, решившего оба случая, будет различаться самое большее на ничтожно малую величину, как нам и было нужно.
Наконец, нам нужно увидеть, что наш экземпляр R-LWE так же сложно решить, как задачу решетки, в нашем случае так же сложно решить, как K-DGS, где K — поле, такое что R — его кольцо целых чисел, другими словами, R=OK (подробнее об определении K-DGS см. определение 2.10 и раздел 2.3.3 в [17]). Эта работа уже была проделана в [17], хотя для того, чтобы сделать это должным образом, нам необходимо дать некоторые разъяснения о различных способах определения распределения R-LWE.
Пусть K — числовое поле, R — кольцо целых чисел. Пусть R∨ — дробный кодифференциальный идеал кольца K (R∨={x∈K|Tr(xR)⊂Z}), и пусть TR=KR/R∨. Пусть q≥2 — целочисленный модуль. Давайте распакуем это. Во-первых, в нашем конкретном случае, когда K является круговым полем с n=2k для некоторого k, мы имеем R=Z[x]/〈xn+1〉, поэтому, в свою очередь, можно видеть, что R∨ изоморфен R. Во-вторых, KR=K⊗QR, который изоморфен Rn, поэтому, рассматривая его компонент за компонентом TR, можно рассматривать его как изоморфный Tn с T=R/Z. С этим из пути мы можем видеть их определение.
С этим из пути мы можем видеть их определение.
Теперь наш постулат состоит в том, что это определение, берущее в качестве Ψ n-мерную сферическую непрерывную гауссиану с параметром ξ (распределение, используемое в [17]), а затем снова повышающее ее до Rq, является более общим определением нашего определения 8 используя Ψ¯ξq, в том смысле, что если мы можем решить экземпляр задачи R-LWE, определенной с распределением в определении 8, мы можем решить экземпляр задачи R-LWE с распределением в определении 14. Можно видеть как единое целое, поскольку сферический гауссиан в Rn можно рассматривать как произведение n независимых гауссианов над R с одним и тем же стандартным отклонением. Затем, по сути, то, что мы делаем в определении 14, умножает a на s, затем делит результат на q (что мы можем сделать, поскольку мы видим элементы в KR, которое является полем) и добавляем распределение ошибок. Затем мы уменьшаем его по модулю R∨, попадая в TR. Теперь, если мы рассмотрим его компонент за компонентом, мы, по сути, вычислили a·s/q, а затем добавили к каждому компоненту выборку Ψξq, так что при повышении его снова до Rq∨ (путем умножения на q и округления) мы получаем, что q (a·s/q)=a·s∈Rq∨ и к каждой компоненте добавлена независимая выборка, взятая из Ψ¯ξq. Следовательно, если ρξn — сферический гауссиан с параметром ξ, то для данного противника, решающего R-LWEΨ¯ξq, легко найти противника, решающего R-LWEρξn.
Следовательно, если ρξn — сферический гауссиан с параметром ξ, то для данного противника, решающего R-LWEΨ¯ξq, легко найти противника, решающего R-LWEρξn.
Таким образом, мы можем применить результат из [17], для которого нам нужно дать два быстрых определения решетки.
Наконец, мы можем дать следующий результат.
В заключение мы увидели, что взломать защиту Схемы шифрования 1 не менее сложно, чем решить задачу R-LWE решения с усеченным дискретным гауссианом, что по крайней мере так же сложно, как решить задачу R-LWE решения с помощью распределение Ψ¯n, что, в свою очередь, не менее сложно, чем решение задачи K-DGS.
5.2. Отсутствие утечки информации
В этом разделе нам нужно убедиться, что злоумышленник не получает никакой дополнительной информации, взаимодействуя с распределенным протоколом. Мы начнем сначала с протокола 1, поскольку противник А не может отличить взаимодействие с протоколом от случайных входных данных. Кроме того, мы также дадим противнику возможность выбирать свои доли секретного ключа и ключей PRSS, поскольку это упрощает игру и служит только для того, чтобы убедиться, что безопасность протокола даже выше, чем обычно требуется.
Для этого нам потребуются следующие вспомогательные леммы о статистическом расстоянии, доказательства которых будут в Приложении B. ценности.
Доказательство.
Мы хотим создать атакующую игру, в которой злоумышленник не может отличить протокол, выполненный правильно, или случайные значения, чтобы показать, что при распределении ничего не происходит ни о секретных ключах, ни об ошибках e.
Пусть C обозначает множество коррумпированных игроков, а B — множество честных игроков. Игра «Атака» работает следующим образом. Предположим, что претендент знает секретный ключ s и KH, такие что C⊇H (ключи, которые противник не знает), которые были сгенерированы безопасным образом. Предположим, что претендент посылает противнику A зашифрованный текст (u,v), а затем A представляет (sC′,KHC,dC′) в качестве вызова, где sC′ — доли секретного ключа поврежденных игроков, KHC — ключи KH такие, что C⊉H (ключи, которые знает A), выбранные A, а dC′ — это доли при расшифровке поврежденных игроков. Затем претендент генерирует согласованные доли на s для игроков, не входящих в C.
Затем претендент генерирует согласованные доли на s для игроков, не входящих в C.
После того, как все эти предварительные действия выполнены, претендент выбирает b ←${0,1} и действует следующим образом:
Если b=0: Претендент использует протокол дешифрования для вычисления долей дешифрования dB′ для честные игроки. Он вычисляет расшифрованное сообщение m и выводит (дБ’, m).
Если b=1: Претендент вычисляет для каждого H такого, что C⊇H, некоторый элемент rH∈IDn равномерно случайным образом, и мы обозначаем как y многочлен от Rq с вектором коэффициентов ∑C⊉HΦKH(u+v) +∑C⊇HrH. Затем претендент генерирует согласованные доли y+m⌊q2⌋ в дБ’ (претендент знает m, поскольку его можно вычислить с помощью протокола, учитывая, что все необходимое известно) и выводит (дБ′,m).
Наконец, A выводит b˜∈{0,1}, означая, считает ли он, что взаимодействовал с протоколом или с симуляцией, и игра завершается.
Ясно, что m будет правильным в обоих случаях, учитывая доказательство теоремы 1, и, кроме того, y+m⌊q2⌋ будет эффективной «расшифровкой» m в том смысле, что каждый коэффициент будет ближе к 0, если mi=0 и ближе к ⌊q2⌋, если mi=1, потому что
Следовательно, нам нужно только увидеть, что дБ’ неотличимы от того, вычисляются ли они с b=0 или с b=1. , как мы видели при доказательстве теоремы 1, находится в интервале [−2nuκ2+κ, 2nuκ2+κ]n. Следовательно, поскольку распределение каждого коэффициента одинаково и независимо, по лемме 2 имеем
9+m⌊q2⌋ вычислительно неразличимы.
, как мы видели при доказательстве теоремы 1, находится в интервале [−2nuκ2+κ, 2nuκ2+κ]n. Следовательно, поскольку распределение каждого коэффициента одинаково и независимо, по лемме 2 имеем
9+m⌊q2⌋ вычислительно неразличимы.
Наконец, складывая все вместе, мы получаем, что выход (дБ’, м) вычислительно неотличим от того, был ли он рассчитан при b=0 или при b=1, поэтому
как мы хотели видеть. □
После теоремы 3 мы увидели, что протокол 1 безопасен только тогда, когда ключи сгенерированы безопасным образом и против пассивного противника, подрывающего t≤u−1 игроков, но стандартно видеть, что тот же протокол безопасен против активного злоумышленник искажает t Причина этого в том, что мы уже видели, что никакая информация не утекает, поэтому нам нужно только убедиться, что противник не может прервать протокол или вызвать неверный вывод. Теперь нам нужно убедиться, что Протокол 2 не пропускает информацию о том, что противник искажает до t=u−1 игроков. Чтобы сделать это, мы еще раз увидим, что злоумышленник не может отличить взаимодействие с протоколом от симуляции, когда претендент заранее устанавливает значения ключей. Доказательство. Мы хотим построить атакующую игру, в которой противник не может отличить правильно выполненный протокол от симуляции, в которой претендент заранее устанавливает значения s, e, aE и KH для всех H. Пусть C обозначает множество коррумпированных игроков, а B — множество честных игроков. Игра «Атака» работает следующим образом. Предположим, что всякий раз, когда коррумпированному игроку нужно выбрать однородное распределение, он отправляет претенденту запрос на получение случайного значения от случайного оракула. Если b=0: Претендент и противник следуют Протоколу 2, чтобы сгенерировать aE,bE и разделить sB’,eB’,KHB,aEB и выходные данные (aE,bE,sB’,eB’,KHB,aEB). Если b=1: Претендент выбирает s,e∼∑uχ, aE ←$Rq и каждый KH ←$Zq и вычисляет bE=aE·s+e. Затем он использует лазейку в схеме фиксации для восстановления (s˚C,e˚C,KNHCs,KNHCe,KHC′,aEC′) и действует следующим образом. Мы разделим объяснение в зависимости от того, что он моделирует для облегчения понимания, но все будет делаться одновременно, следуя потоку информации, показанному в таблице 3. Для «генерации» s претендент будет использовать ключи KNHCs (все они ему известны, учитывая, что они были сгенерированы с помощью запросов к случайному оракулу через претендента) для восстановления sC, вклад коррумпированных игроков в с. Для «генерации» e претендент действует так же, как и для генерации s. Для «генерации» KH претендент выбирает случайные значения в Zq для KHB′ (первый шаг) и фиксирует их. Затем он получит KHC от противника (доли KH, относящиеся к коррумпированным игрокам) и вычислит согласованные доли Shamir KHB, чтобы игроки разделили KH. Затем, как и в протоколе, претендент рассылает доли KHB всем игрокам, не входящим в H. Для «генерации» aE претендент выбирает случайные значения в Rq для aEB (первый шаг) и фиксирует их. Затем он получит aEC (доли aE, относящиеся к коррумпированным игрокам) и вычислит согласованные доли Shamir aEB, чтобы игроки разделили aE. Затем, как и в протоколе, претендент рассылает доли aEB всем игрокам. Для «генерации» bE претендент выводит bE в конце протокола. Затем претендент выводит (aE,bE,sB′,eB′,KHB,aEB). Наконец, A выводит b˜∈{0,1}, означая, считает ли он, что взаимодействовал с протоколом или с симуляцией, и игра завершается. Понятно, что поток информации одинаков в обоих случаях и что значения будут как правильными, так и тем, что претендент выбрал заранее, поэтому нам просто нужно убедиться, что противник не может различить значения, полученные при b=0 от полученных при b=1. Для s (и e) ясно, что они неразличимы, так как мы использовали лазейку в схеме фиксации, чтобы установить значения, необходимые до отправки каких-либо сообщений от противника к претенденту. Более того, мы знаем, что никакой утечки информации в NIVSS не было, так как из-за лемм 2 и 3 мы знаем, что никакой утечки информации не было, как при доказательстве теоремы 3. Для KH (и, в свою очередь, aE, так как они аналогичны) нужно убедиться, что противник не может отличить от KHB′, сгенерированных протоколом, или от случайных в Zq. Наконец, суммируя все, мы получаем, что (aE,bE,sB′,eB′,KHB,aEB) неразличимы, имеем ли мы b=0 или b=1, поэтому как мы хотели видеть. □ Как и в разделе 4, мы также доказали эквивалент этой последней теоремы для активного противника, однако мы не будем использовать результат для реализации по причинам, которые мы изложим в разделе 6.1. Доказательство можно найти в Приложении A.2. Доказав безопасность каждого протокола в отдельности, нам нужно только увидеть, что использование обоих протоколов вместе дает нам схему шифрования, которая семантически безопасна. Первым шагом для реализации является поиск хороших параметров, гарантирующих безопасность конкретного экземпляра проблемы R-LWE. Устанавливаем параметр безопасности λ=100. Нам нужно найти следующие параметры: n, q, κ и ξ, которые затем позволят нам вычислить ID и IKG. Сначала мы оставим все в зависимости от n и q, а затем воспользуемся конкретной сложностью экземпляра задачи R-LWE, чтобы исправить n и q. Пусть n=2β и q∈Z>0. Используя условия на ID из теоремы 1, получаем, что Для нахождения ξ воспользуемся следующей леммой, доказательство которой находится в Приложении B. Используя оценку по определению 13 и лемму 4, можно получить следующую оценку: что при выделении ξ дает нам следующую оценку: Отсюда мы возьмем равенство, так как при фиксированном q чем больше стандартное отклонение, тем больше сложность этого конкретного случая решения проблемы R-LWE. Теперь мы можем найти n и q, используя оценщик твердости LWE, который при заданных n,q,α выводит конкретную твердость этого конкретного экземпляра. Мы зададим n как степень двойки, поскольку это позволяет нам использовать более эффективные алгоритмы умножения, а q — как простое число, близкое к степени двойки. Используя это, мы реализовали алгоритм Python для нахождения этих параметров. Код можно найти в репозитории в Приложении C. Это дало следующие результаты в качестве параметров для u=7 и t=2 и более 100 бит безопасности, как видно из таблицы 4. В этом коде также выполняется вычисление параметров для случая активного противника на этапе генерации ключа с использованием условий теоремы A1. п = 8192. Это, как мы увидим из результатов в разделе 6.3, подрывает жизнеспособность протоколов, поэтому мы считаем наше основное предложение безопасным от злоумышленника, который действует пассивно на этапе генерации ключа и активно на этапе дешифрования. Мы приняли несколько решений по внедрению, которые необходимо обсудить. Во-первых, мы закодировали не действительно интерактивный протокол между u разными игроками, а скорее симуляцию, в которой один процессор вычисляет все шаги, имитирующие взаимодействие, в том смысле, что протоколы разделены по шагам между фазами связи, где все вычисления могут быть выполнены без необходимость взаимодействия с другими объектами. Затем программа вычисляет, сколько времени стоит каждый шаг для каждого игрока, и выбирает максимальное значение в качестве «официального» времени для этого шага. Поскольку мы хотим только приблизительно проанализировать, насколько жизнеспособны наши протоколы, это приблизительное значение работает для нас. Это приближение также означает, что выполнение симуляции длится значительно дольше, чем «реальное время» выполнения, что ограничивает нас количеством игроков, которых мы можем разумно использовать. Во-вторых, чтобы получить наиболее компактную форму совместного использования секрета Шамира, мы использовали Шамир над полем Zq вместо того, чтобы встраивать его в Q. В-третьих, что касается реализации PRF, мы использовали основной результат из [20], в котором говорится, что код аутентификации сообщений на основе хэшей (HMAC) является PRF при условии, что основная функция сжатия является PRF. Чтобы обеспечить выполнение этого условия, мы использовали HMAC, основанный на SHA-3. Наконец, что касается схемы фиксации, которую мы использовали для протокола генерации ключей, мы использовали хэш сообщения, которое мы хотим отправить, объединенным со случайной строкой. Мы использовали SHA-2, потому что, насколько нам известно, он достаточно безопасен. Однако в случае необходимости его можно заменить на более безопасный вариант. Кроме того, нам нужно было использовать схему обязательств только после первого раунда, когда каждый игрок устанавливает свои значения. Это связано с тем, что как только все значения установлены и все доли отправлены, вклады противника больше не нужны, поскольку честные игроки уже могут генерировать большинство правильных значений. В этом заключительном разделе мы обсудим результаты, полученные нами в результате выполнения кода для моделирования обоих протоколов. Вы можете найти код в репозитории, указанном в Приложении C. Спецификации системы, в которой мы выполнили программы, приведены в Таблице 5. Кроме того, мы использовали следующие библиотеки C: FLINT (Fast Library for Number Theory) для облегчения вычисления в Rq, который, в свою очередь, использует библиотеки GMP и MPFR для работы с числами с множественной точностью и библиотеку OpenSSL для функций, связанных с криптографией, таких как хэши или HMAC. Из того, что мы видели к этому моменту, есть две основные зависимости: рост времени по отношению к порогу t и рост времени по отношению к размерности решетки. Это так, потому что порог определяет минимально необходимое количество игроков (и наоборот, учитывая количество игроков, мы можем получить максимально допустимый порог), в зависимости от того, защищаемся ли мы от активного или пассивного противника. Как мы видели в разделе 6.1, для модели злоумышленника при заданном n мы можем найти остальные параметры, которые делают протокол безопасным (принимая во внимание, что существует минимальное n, для которого этот анализ работает). Что касается зависимости от t, анализ протоколов теоретически позволяет увидеть, что при выполнении либо PRSS, либо NIVSS имеется ut разных ключей KH, а это означает, что количество сложений асимптотически растет со значением ut. Что касается зависимости от n, то при наличии умножения полиномов в обоих протоколах, которое реализовано с помощью алгоритма Карацубы, масштабируемого порядка nlog2(3)>n1,5, время асимптотически растет с этим значением . Результаты, полученные для зависимости от n, которые можно увидеть на рисунке 1, показывают ожидаемые результаты только на этапе дешифрования против пассивного противника. Для других случаев мы видим линейное или практически линейное поведение для диапазона значений n, которые нас интересуют для реальных приложений. Это связано с тем, что протоколы должны выполнять гораздо большее количество дополнений, чем продуктов, и эта разница оказывается достаточно высокой, чтобы линейный рост добавления компенсировал рост продукта при этих значениях n. Наконец, мы хотим обсудить жизнеспособность протоколов. В заключение мы хотели бы обобщить ограничения, которые имеет эта работа, и то, как ее можно улучшить в будущих работах, а также дать некоторое представление о некоторых возможных других применениях за пределами изложенные выше. С точки зрения конструкции наше предложение имеет два основных ограничивающих фактора: во-первых, тот факт, что мы вычисляем шумы утопления с помощью методов PRSS и NIVSS, означает, что время вычислений будет увеличиваться асимптотически экспоненциально с количеством игроков в активном противнике. Что касается реализации, мы хотели бы повторить, что предлагаемые нами коды являются доказательством концепции приблизительной жизнеспособности и ни в коем случае не попыткой создать вычислительно безопасную и эффективную программу. Наконец, мы также хотели бы отметить тот факт, что даже если представленные протоколы были задуманы с идеей их совместного использования, их доказательства безопасности независимы, и поэтому их можно использовать по отдельности. Это означает, что в случае, когда TTP можно доверить генерацию ключа, можно использовать только протокол расшифровки, а затем сделать процесс полностью неинтерактивным. Кроме того, несмотря на то, что протокол генерации ключей в большей степени адаптирован к потребностям схемы шифрования, было бы несложно выделить основные принципы генерации различных типов элементов, поэтому его легко обобщить с помощью аналогичного доказательства безопасности. Концептуализация, Р.М. и П.М.; методика, Р.М. и П.М.; программное обеспечение, FA и RM; валидация, Ф.А.; формальный анализ, Ф.А., Р.М. и П.М.; расследование, Ф.А., Р.М. и П.М.; ресурсы, Ф.А., Р.М. и П.М.; написание — подготовка первоначального проекта, F.A.; написание — обзор и редактирование, Ф.А., Р.М. и П.М.; надзор, П.М.; администрирование проекта, Ф.А., Р.М. и П.М.; приобретение финансирования, P.M. Все авторы прочитали и согласились с опубликованной версией рукописи. Это исследование было частично профинансировано проектом PROMETHEUS Европейского Союза (Программа исследований и инноваций Horizon 2020, грант 780701) и Министерством экономики и конкурентоспособности Испании в рамках проекта MTM2016-77213-R. Неприменимо. Неприменимо. Неприменимо. Авторы заявляют об отсутствии конфликта интересов. В данной рукописи используются следующие сокращения: Теперь у нас все еще есть rE,ev,eu∼χ, но для t вкладов мы можем только гарантировать, что они находятся в 2·IKG, так что мы получаем, что Кроме того, учитывая, что имеется ut ключей KH, мы знаем, что Складывая оба результата, мы получаем, что как мы хотели видеть. Наконец, нам просто нужно увидеть, что когда клиент реконструирует, действительно есть большинство правильных результатов, и это напрямую вытекает из наличия не более t испорченных игроков; следовательно, будет большинство подмножеств t+1 игроков, где все они честны и, таким образом, выводят правильную расшифровку. □ Как и в разделе 4, то же доказательство работает против пассивного противника, развращающего до t=u−1 игроков. Однако в случае работы с активным противником на этапе генерации ключа, чтобы иметь действительно правильную схему, мы должны видеть, что протокол не может быть остановлен никакими действиями злоумышленника. Политика работает следующим образом, после остановки протокола игроки просматривают возникшие споры, а затем «устраняют» всех причастных к ним игроков, в том смысле, что новое выполнение протокола генерации ключей начнется без обоих игроков, участвующих в каждом споре, а в случае, если игрок участвует более чем в одном споре, будет проанализирован только первый. Эта политика гарантирует, что протокол будет давать правильный вывод с не более чем t остановок, поскольку между честными игроками не может возникнуть спор, и учитывая, что безопасность схемы основана только на предположении, что существует по крайней мере один вклад в s и e после распределения вывод не вызывает проблем. Чтобы иметь возможность доказать безопасность, когда генерация ключей направлена против активного противника, нам нужно только переформулировать теорему следующим образом. Доказательство аналогично доказательству теоремы 1. Теперь мы докажем, что генерация ключей не дает утечки информации при воздействии на активного противника, подкупающего до t Доказательство. Мы хотим построить атакующую игру, в которой противник не может отличить правильно выполненный протокол от симуляции, в которой претендент заранее устанавливает значения s, e, aE и KH для всех H. Пусть C обозначает множество коррумпированных игроков, а B — множество честных игроков. Игра «Атака» работает следующим образом. Предположим, что всякий раз, когда коррумпированному игроку нужно выбрать однородное распределение, он отправляет претенденту запрос на получение случайного значения от случайного оракула. Пусть CC=Commit(s˚C,e˚C,KNHCs,KNHCe,KHC′,aEC′) вызов, выводимый A, первый шаг взаимодействия в протоколе 2, как мы можем видеть в таблице 3. Тогда претендент выбирает b ←${0,1} и действует следующим образом: Если b=0: Претендент и противник следуют протоколу 2 для генерации aE,bE и долей sB′,eB′,KHB,aEB и выходов (aE,bE,sB′,eB′,KHB,aEB ). Если b=1: Претендент выбирает s,e∼∑uχ, aE ←$Rq и каждый KH ←$Zq и вычисляет bE=aE·s+e. Затем он использует лазейку в схеме фиксации для восстановления (s˚C,e˚C,KNHCs,KNHCe,KHC′,aEC′) и действует следующим образом. Мы разделим объяснение в зависимости от того, что он моделирует для облегчения понимания, но все будет делаться одновременно, следуя потоку информации, показанному в таблице 3. Для «генерации» s претендент будет использовать ключи KNHCs (все они ему известны, поскольку он/она контролирует более t игроков), чтобы восстановить sC, вклад коррумпированных игроков в s . С помощью этой информации претендент может вычислить sB вклад честных игроков в s так, что s=sC+sB. Вычислив эти значения, претендент приступает к протоколу. Для «генерации» e претендент действует так же, как и для генерации s′. Для «поколения» KH претендент восстанавливает KHC (поскольку он контролирует более t игроков) вклад коррумпированных игроков в KH. С помощью этой информации претендент может вычислить KHB вклад честных игроков таким образом, что KH=KHC+KHB для всех H. Вычислив эти значения, претендент приступает к выполнению протокола. Для «генерации» aE претендент восстанавливает aEC (поскольку он контролирует более t игроков) вклад коррумпированных игроков в aE. С помощью этой информации претендент может вычислить aEB вклад честных игроков таким образом, что aE=aEC+aEB. Для «генерации» bE претендент выводит bE в конце протокола. Затем претендент выводит (aE,bE,sB′,eB′,KHB,aEB). Наконец, A выводит b˜∈{0,1}, означая, считает ли он, что взаимодействовал с протоколом или с симуляцией, и игра завершается. Понятно, что поток информации одинаков в обоих случаях и что значения будут правильными и теми, что претендент выбрал заранее, поэтому нам просто нужно убедиться, что противник не может различить значения, полученные при b=0 от полученных при b=1. Мы можем видеть, что они неразличимы, поскольку претендент использует лазейку в схеме фиксации, чтобы получить значения, необходимые до того, как любое сообщение будет отправлено от претендента противнику. Более того, опять же, мы знаем, что никакой утечки информации в НИВСС не было по тем же рассуждениям из доказательства теоремы 4. Следовательно, (aE,bE,sB′,eB′,KHB,aEB) неразличимы для противника независимо от того, были ли они вычислены с b=0 или b=1, поэтому как мы хотели видеть. Доказав безопасность каждого протокола в отдельности, нам нужно только увидеть, что совместное использование обоих протоколов по-прежнему дает нам схему шифрования, которая семантически безопасна. Доказательство. Что мы хотим увидеть, так это то, что при наличии эффективного противника A, который имеет существенное семантическое преимущество в безопасности, мы можем создать эффективного противника B с доступом к A, который, учитывая экземпляр проблемы R-LWE с принятием решений, может решить это с вероятностью, незначительно превышающей 12. Пусть (a¯i,b¯i)∈Rq×Rq — пример решения R-LWE задачи. Что нам нужно, чтобы сделать B, так это вывести, является ли полиномиальное количество экземпляров образцами распределения As, χ или равномерного распределения по Rq × Rq, другими словами, мы хотим знать, является ли b¯i=a¯i· s¯+e¯ для некоторых s¯∈Rq и e¯⟵χ. Обратите внимание, что любой противник A, нарушающий семантическую безопасность, может относиться к одному из двух типов. Либо A имеет существенное семантическое преимущество в безопасности по сравнению со схемой шифрования, когда (aE,bE) генерируются независимо равномерно случайным образом (вместо того, чтобы bE=aE·s+e), либо нет. Для этих случаев мы построим двух разных противников. Сначала предположим, что A имеет незначительное семантическое преимущество в безопасности по сравнению со схемой шифрования, когда (aE,bE) генерируются независимо равномерно случайным образом. Пусть (a1,b1) — пример задачи R-LWEχ, тогда определим следующую атакующую игру. Тогда B будет работать следующим образом. Получив экземпляры, он выбирает (a¯1,b¯1) и выполняет атакующую игру 1 с A полиномиальное количество раз. Затем он вычисляет преимущество Из того, как мы определили противника A, мы знаем, что SSAdv[A,S] нельзя пренебречь, если экземпляры следуют распределению As,χ, тогда SSAdv1∗[A,S] не будет пренебрежимо малым, и если экземпляры однородны по Rq×Rq, тогда SSAdv1∗[A,S] будет пренебрежимо малым. Теперь предположим, что A имеет существенное семантическое преимущество в безопасности по сравнению со схемой шифрования, когда (aE,bE) генерируются независимо равномерно случайным образом. Пусть снова (a1,b1) и (a2,b2) — два случая задачи R-LWEχ, тогда мы определим следующую атакующую игру. Тогда B будет работать следующим образом. Получив экземпляры, он выбирает два из них (a¯1,b¯1) и (a¯2,b¯2) и выполняет атакующую игру 2 с A полиномиальное количество раз. Затем он вычисляет преимущество Из того, как мы определили противника A, мы знаем, что, поскольку SSAdv[A,S] нельзя пренебречь, если экземпляры следуют распределению As,χ, тогда SSAdv2∗[A,S] не будет пренебрежимо малым, и если экземпляры равномерны по Rq×Rq, то SSAdv2∗[A,S] будет пренебрежимо малым, так как если b¯i равномерно случайны, то v2 не зависит от открытого ключа и mb22. Все соответствующие коды для реализации можно найти в следующем репозитории GitHub, последнее обновление сделано 20 декабря 2021 г.: https://github.com/FerranAlborch/Implementation-RLWE-based-distributed-key-generation-and-threshold-decryption. Рисунок 1. Время моделирования для n = 256 512 1024 2048 4096 8192. Рисунок 1. Время моделирования для n = 256 512 1024 2048 4096 8192. Таблица 1. Уровень развития. Таблица 1. Уровень развития. Table 2 Протокол расшифровки. Таблица 2. Протокол расшифровки. Таблица 3. Протокол генерации ключей. Таблица 3. Протокол генерации ключей. Таблица 4. Параметры для безопасной реализации. Таблица 4. Параметры для безопасной реализации. 875 Table 5. Технические характеристики системы. Таблица 5. Технические характеристики системы. Таблица 6. Сравнение времени между активным и пассивным противником. Таблица 6. Сравнение времени между активным и пассивным противником. Примечание издателя: MDPI остается нейтральным в отношении юрисдикционных претензий в опубликованных картах и институциональной принадлежности. Ethereum стал второй по величине криптовалютой по рыночной капитализации, во многом благодаря поддержке смарт-контрактов, которые лежат в основе растущей экосистемы децентрализованных приложений (dapps) и платформ децентрализованных финансов (DeFi). Но у него есть одна проблема: он медленный и дорогой в использовании из-за постоянно высоких комиссий за транзакции. Пока сообщество Эфириума ждет развертывания запланированных обновлений сети, которые решат эти проблемы, появились решения для масштабирования, которые сделают транзакции Эфириума быстрее и дешевле. Optimism — одно из таких решений для масштабирования. Оптимизм ускоряет транзакции Ethereum и снижает их стоимость, проводя их на другом блокчейне с использованием передовых методов сжатия данных. Особая изюминка методологии масштабирования Optimism заключается в ее названии: она использует технику, называемую оптимистическими сверлениями, в соответствии с которой несколько транзакций «свертываются» в одну транзакцию, рассчитываются в другой цепочке блоков, а квитанции возвращаются в основную цепочку блоков Ethereum. 👩💻 Протокол 👩💻 Мы получили массу удовольствия от времени, потраченного на проектирование, создание и эксплуатацию оптимистичного накопительного пакета. Извлеченные уроки будут обобщены в следующей важной вехе протокола: в том, что мы сейчас называем «OP 1.0». — Optimism (✨🔴_🔴✨) (@optimismPBC) 31 января 2022 г. Оптимистичные накопительные пакеты — это тип накопительного пакета, который «оптимистично» предполагает, что все транзакции в агрегированном пакете действительны. Это экономит время, поскольку отдельные транзакции не должны представляться с прямым подтверждением их действительности. У валидаторов в сводке есть неделя, чтобы запросить всю сводку, если они считают, что она содержит мошеннические данные. Панель инструментов Dune Analytics показывает, что Optimism снижает комиссию за транзакции Ethereum (также известную как плата за газ) в ошеломляющие 129 раз. Он поддерживается платформами DeFi, такими как Synthetix и Uniswap. Optimism был представлен в июне 2019 года, а тестовая сеть была выпущена в октябре 2019 года. Только в январе 2021 года была запущена альфа-основная сеть, и только в октябре 2021 года Optimism запустила версию основной сети Alpha, которая была совместима. с виртуальной машиной Ethereum. Открытая основная сеть запущена в декабре 2021 г. Optimism — это, по сути, большой список транзакций, который можно только добавить. Все его свернутые блоки хранятся в смарт-контракте Ethereum, называемом канонической цепочкой транзакций. Если пользователь не отправит свою транзакцию непосредственно в каноническую цепочку транзакций, новые блоки создаются чем-то, называемым секвенсором. Этот секвенсор мгновенно подтверждает действительные транзакции, а затем создает и выполняет блоки на уровне 2 Optimism — блокчейне, который находится поверх блокчейна L1, в данном случае Ethereum. Эти блоки представляют собой «свертки» — пакеты транзакций Ethereum. Секвенсор еще больше сжимает эти данные, чтобы уменьшить размер транзакции (и, таким образом, сэкономить деньги), а затем отправляет данные транзакции обратно в Ethereum. Программное обеспечение 2-го уровня Optimism разработано таким образом, чтобы максимально имитировать код Ethereum. Например, он использует ту же виртуальную машину, что и Ethereum, и взимает плату за газ таким же образом (хотя и по более низкой ставке благодаря своему оптимистичному решению по объединению). Поскольку Ethereum и Optimism очень похожи внутри, вы можете отправить любой актив ERC-20 — криптовалюту, соответствующую общему стандарту токена Ethereum — между двумя сетями. Оптимизм лучше всего понимать как одно из нескольких решений, пытающихся решить проблему раздувания состояния Ethereum. Сеть Ethereum способна взорваться, и до тех пор, пока обновления основного блокчейна не спасут положение, масштабирующие решения, такие как Optimism, позволяют индустрии децентрализованных финансов Ethereum расти и оставаться доступной для тех, кто не может позволить себе высокие комиссии за транзакции. Протокол — не единственное решение для масштабирования, использующее оптимистичные свертки. Arbitrum и Boba Network также используют эту технику, чтобы помочь пользователям Ethereum сэкономить на комиссиях. Свертки с нулевым разглашением, еще один популярный тип свертывания, используются Loopring, Immutable X и ZKSync. Как и у Arbitrum, у Optimism нет собственной криптовалюты для оплаты газа. Он использует ETH, как и Arbitrum. Как и Arbitrum, Optimism находится в стадии бета-тестирования и еще не полностью децентрализован. Чтобы использовать Optimism, вам необходимо внести свои токены ETH или ERC-20 в мост токенов Optimism. Это позволяет вам совершать транзакции на Ethereum через Optimism. Вы можете конвертировать свои токены обратно в сеть Ethereum, когда закончите. Чтобы внести свои жетоны, вам необходимо внести их через шлюз оптимизма. Вы можете подключиться к шлюзу через кошелек Web3, такой как MetaMask. Компания Optimism сообщила, что для вывода средств потребуется неделя и 52,72 доллара США. Эта задержка является особенностью недельного испытания, заложенного в оптимистическом сведении Optimism. После того, как вы внесли средства на Optimism, вы можете использовать их в поддерживаемых децентрализованных приложениях. Uniswap, например, позволяет вам торговать через Optimism, чтобы сэкономить на комиссиях. Все, что вам нужно сделать, это выбрать «Оптимизм» в меню сетей; затем вы можете торговать как обычно. У Optimism достаточно средств для продолжения своей работы; в марте 2022 года он закрыл раунд финансирования серии B на сумму 150 миллионов долларов, возглавляемый Andreessen Horowitz и Paradigm, в результате чего стартап был оценен в 1,65 миллиарда долларов. Его дорожная карта включает в себя обновления протокола Optimism, такие как защита от сбоев следующего поколения, сегментированные сводки и децентрализованный секвенсор. Последний важный момент: пока проект находится в стадии бета-тестирования, команда сохраняет определенный контроль над секвенсором — технологией, ответственной за создание блоков на Optimism. Оптимизм исторически был более централизованным, чем Эфириум, чьи разработчики не имеют возможности, например, приостановить блокчейн или внести в белый список определенных валидаторов. Однако Optimism сделала большой шаг к децентрализации в апреле 2022 года, запустив DAO под названием Optimism Collective для финансирования общественных благ и управления протоколом. Он также начал раздавать недавно созданные токены OP пользователям Optimism и другим людям, которые могли бы помочь продвинуть DAO — и децентрализованное будущее Optimism — вперед. Это пятая часть серии статей о модели случайного оракула. Часть 1: Введение Около восьми лет назад я решил написать очень неформальную статью о конкретном методе криптографического моделирования, который называется «модель случайного оракула». Это было еще в старые добрые времена 2011 года, когда была более невинная и мягкая эпоха криптографии. Тогда никто не предвидел, что вся наша стандартная криптография окажется пронизанной ошибками; вам не нужно было напоминать, что «крипто означает криптографию». Люди даже использовали Биткойн, чтобы покупать вещи. Этот первый случайный пост оракула каким-то образом породил три продолжения, каждое из которых нелепее предыдущего. Думаю, в какой-то момент мне стало стыдно за все это — если честно, это довольно глупо — поэтому я как бы забросил его незаконченным. Чтобы дать вам некоторый контекст, позвольте мне кратко напомнить вам, что такое модель случайного оракула и почему вы должны о ней заботиться. (Хотя вам лучше просто прочитать серию.) Модель случайного оракула — это сумасшедший способ моделирования (обоснования) хеш-функций, в котором мы предполагаем, что это на самом деле случайные функции, и используем это предположение для доказательства того, что о криптографических протоколах доказать гораздо труднее без такого модель. Почти вся «доказуемая» криптография, которую мы используем сегодня, зависит от этой модели, а это означает, что многие из этих доказательств были бы поставлены под сомнение, если бы они были «ложными». И чтобы подразнить остальную часть этого поста, я процитирую заключительные абзацы части 4, которая заканчивается следующим образом: Видите ли, мы всегда знали, что эта поездка не будет длиться вечно, мы просто думали, что у нас есть больше времени. Как и было обещано, этот пост будет об этом крахе и о том, что он означает для криптографов, специалистов по безопасности и всех нас. Во-первых, чтобы сделать этот пост немного более самодостаточным, я хотел бы напомнить некоторые основы, которые я рассмотрел ранее в этой серии. Вы можете смело пропустить эту часть, если вы только что оттуда. Как обсуждалось в первых разделах этой серии, хеш-функции (или алгоритмы хеширования) — это стандартный примитив, который используется во многих областях информатики. Они принимают некоторый ввод, как правило, строку переменной длины, и многократно выводят короткий «дайджест» фиксированной длины. Криптографическое хеширование берет этот базовый шаблон и добавляет некоторые важные безопасность свойства которые нам нужны для криптографических приложений. Наиболее известны такие свойства, как устойчивость к столкновениям, которые необходимы для таких приложений, как цифровые подписи. Но хеш-функции появляются повсюду в криптографии, иногда в неожиданных местах — от шифрования до протоколов с нулевым разглашением — и иногда эти системы требуют более сильных свойств. Иногда это может быть сложно выразить в формальных терминах: например, многие протоколы требуют хэш-функции для получения чрезвычайно «случайного» вывода.* На заре доказуемой безопасности криптографы поняли, что идеальная хэш-функция будет вести себя как «случайная функция». Этот термин относится к функции, которая равномерно выбирается из набора 91 218 всех возможных 91 219 функций, имеющих соответствующую спецификацию ввода/вывода (домен и диапазон). Итак, мы не используем случайные функции для реализации нашего хеширования. В «реальном мире» мы используем странные функции, разработанные бельгийцами или Агентством национальной безопасности, вроде SHA256, SHA3 и Blake2. Эти функции поставляются с невероятно быстрыми и крошечными алгоритмами для их вычисления, большинство из которых занимают несколько десятков строк кода или меньше. Они, конечно, не случайны, но, насколько мы можем судить, выход выглядит как довольно запутанным. Тем не менее, разработчики протоколов продолжают стремиться к безопасности, которую действительно случайная функция может обеспечить их протоколу. Что если, спросили они, мы попытаемся разделить разницу. Как насчет того, чтобы мы смоделировали наши хеш-функции, используя случайные функции — просто ради написания наших доказательств безопасности — а затем, когда мы перейдем к , реализуем (или «создадим экземпляр») наши протоколы, мы начнем использовать эффективные хэш-функции, такие как SHA3? Естественно, эти доказательства не будут в точности применимы к реальному протоколу в том виде, в котором он был создан, но они все равно могут быть довольно хорошими. Доказательство, использующее эту парадигму, называется доказательством в модели случайного оракула или ПЗУ. Для полной механики того, как работает ПЗУ, вам придется вернуться и прочитать серию с самого начала. Что вам, , нужно знать прямо сейчас, так это то, что доказательства в этой модели должны каким-то образом обходить тот факт, что вычисление случайной функции занимает экспоненциальное время. Это означает, что каждый раз, когда одна из сторон хочет вычислить функцию, она не делает этого сама. Вместо этого они обращаются к третьему лицу, «случайному оракулу», который хранит гигантскую таблицу входных и выходных данных случайных функций. На высоком уровне модель выглядит примерно так: Поскольку все стороны в системе «разговаривают» с одним и тем же оракулом, все они получают один и тот же результат хеширования, когда просят его хешировать данное сообщение. Это довольно хороший пример того, что происходит с реальной хэш-функцией. Использование внешнего оракула позволяет нам «похоронить» затраты на оценку случайной функции, так что никому больше не нужно тратить экспоненциальное время на ее оценку. Совершенно верно! Однако — я думаю, что есть несколько очень важных вещей, которые вы должны знать о модели случайного оракула, прежде чем списывать ее со счетов как очевидно бессмысленную: 1. Конечно, все знают, что доказательства случайного оракула не являются «настоящими». Большинство добросовестных разработчиков протоколов признают, что доказательство безопасности в модели случайного оракула , а не на самом деле означает, что это будет безопасно «в реальном мире». Другими словами, тот факт, что случайные доказательства модели оракула являются своего рода подделкой, , а не какая-то глубокая тайна, о которой я вам расскажу. 2. И вообще: доказательства ПЗУ обычно считаются полезной эвристикой. Для тех, кто не знаком с этим термином, «эвристика» — это слово, которое взрослые используют, когда собираются обезопасить свои сбережения с помощью криптографии, которую они ничего не могут доказать. Я шучу! Фактически, случайные доказательства оракула все еще весьма ценны. В основном потому, что они часто помогают нам обнаруживать ошибки в наших схемах. То есть, хотя случайное доказательство оракула не означает безопасности в реальном мире, невозможность написать один обычно является красным флажком для протоколов. Более того, наличие доказательства ПЗУ, как мы надеемся, является индикатором того, что «кишки» протокола в порядке, и что любые возникающие в реальном мире проблемы будут как-то связаны с хэш-функцией. 3. Схемы, проверенные ПЗУ, имеют довольно приличный послужной список на практике. Если бы пруфы ПЗУ каждый день выбрасывали нелепо сломанные схемы, мы бы, наверное, отказались от этой техники. Тем не менее, мы почти каждый день используем криптографию, проверенную (только) в ПЗУ, и в основном она работает нормально. Это не означает, что ни одна из проверенных ПЗУ схем никогда не была нарушена при создании экземпляра с помощью определенной хэш-функции. 4. В течение многих лет многие люди верили, что ПЗУ действительно можно сохранить. Эта надежда была вызвана тем фактом, что схемы ПЗУ, как правило, работали довольно хорошо при реализации с сильными хэш-функциями, и поэтому, возможно, все, что нам нужно было сделать, это найти хэш-функцию, которая была бы «достаточно хороша», чтобы сделать доказательства ПЗУ осмысленными. . Некоторые теоретики надеялись, что причудливые методы вроде криптографической обфускации можно будет каким-то образом использовать для создания конкретных алгоритмов хеширования,1218 вел себя достаточно хорошо, чтобы можно было создать (некоторые) доказательства ПЗУ. Таково состояние ПЗУ, или, по крайней мере, так оно было до конца 1990-х годов. Мы знали, что эта модель была искусственной, и тем не менее она упорно отказывалась взрываться или давать совершенно бессмысленные результаты. А потом, в 1998 году, все пошло наперекосяк. CGH доказала, что на самом деле существуют криптографические схемы, которые могут быть полностью безопасными в модели случайного оракула, но которые — ужасно — становятся катастрофически небезопасными в ту минуту, когда вы создаете экземпляр хэш-функции с любой конкретной функцией . Это действительно пугающий результат, по крайней мере, с точки зрения доказуемого сообщества безопасности. Одно дело знать в теории , что ваши доказательства могут быть не такими сильными. Прежде чем мы перейдем к подробностям CGH и связанным с ним результатам, несколько предостережений. Во-первых, CGH во многом является результатом теории . Криптографические «контрпримеры», которые решают эту проблему, обычно не выглядят как настоящие криптосистемы, которые мы будем использовать на практике, хотя более поздние авторы предложили несколько более «реалистичных» вариантов. На самом деле они созданы для того, чтобы делать очень искусственные вещи, которые никогда не сможет сделать ни одна «настоящая» схема. Это может привести к тому, что читатели отклонят их на основании искусственности. Проблема с этой точкой зрения в том, что взгляды не являются особо научным способом судить о схеме. И «реально выглядящие», и «искусственные» схемы являются, если доказано, что они верны, действительными криптосистемами. Еще одно преимущество этих «искусственных» схем заключается в том, что они относительно легко объясняют основные идеи. В качестве дополнительного примечания по этому поводу: вместо того, чтобы объяснять саму CGH, я собираюсь использовать формулировку того же основного результата, который был предложен Маурером, Реннером и Холенштейном (MRH). Основная идея контрпримеров в стиле CGH состоит в том, чтобы сконструировать «надуманную» схему, которая надежно хранится в ПЗУ, но полностью разрушается, когда мы «создаем экземпляр» хэш-функции, используя любую конкретную функцию, то есть функцию, которая имеет реальное описание и могут быть эффективно оценены участниками протокола. Хотя методы CGH могут применяться с большим количеством различных типов криптосистем, в этом объяснении мы собираемся начать наш пример с относительно простого типа системы: схемы цифровой подписи. Вы, возможно, помните из предыдущих эпизодов этой серии, что обычная схема подписи состоит из трех алгоритмов: генерация ключа , подписание и проверка . Алгоритм генерации ключей выводит открытый и секретный ключи. Подписание использует секретный ключ для подписи сообщения и выводит подпись. Проверка принимает полученную подпись, открытый ключ и сообщение и определяет, является ли подпись действительной : она выводит «Истина», если подпись проверена, и «Ложь» в противном случае. Традиционно мы требуем, чтобы схемы подписи были (по крайней мере) экзистенциально не поддающимися подделке при атаке выбранного сообщения или UF-CMA. Это означает, что мы рассматриваем эффективного (с полиномиальным временем) злоумышленника, который может запрашивать подписи на выбранных сообщениях, которые создаются «оракулом подписи», содержащим секретный ключ подписи. Мы ожидаем, что безопасная схема состоит в том, что даже при таком доступе ни один злоумышленник не сможет придумать подпись на некоторых новое сообщение о том, что она не просила подписывающего оракула подписать за нее, за исключением незначительной вероятности. Объяснив эти основы, давайте поговорим о том, что мы собираемся с этим делать. Это будет включать в себя несколько шагов: Шаг 1: Начните с какой-нибудь существующей безопасной схемы подписи. На самом деле не имеет значения, с какой схемы подписи мы начнем, если мы можем предположить, что она безопасна (в соответствии с определением UF-CMA, описанным выше). Эта существующая схема подписи будет использоваться в качестве строительного блока для новой схемы, которую мы хотите построить.*** Мы назовем эту схему S . Шаг 2: Мы будем использовать существующую схему S в качестве строительного блока для создания «новой» схемы подписи, которую мы назовем . Построение этой новой схемы в основном будет состоять из добавления странных наворотов к алгоритмам исходной схемы S. Шаг 3: Подробно описав работу , мы утверждаем, что она полностью безопасно в ПЗУ. Шаг 4: Наконец, мы продемонстрируем, что полностью сломан, когда вы создаете случайный оракул с любой конкретной хэш-функцией , независимо от того, насколько «безопасной» она выглядит. Короче говоря, мы покажем, что если вы замените случайный оракул реальной хэш-функцией, получится простая атака, которая всегда приводит к успеху в подделке подписей. Начнем с объяснения того, как это работает. Чтобы построить нашу надуманную схему, мы начнем с существующей защищенной (в смысле UF-CMA) схемы подписи S . Нам нужно построить эквивалентные три алгоритма для нашей новой схемы. Чтобы облегчить жизнь, наша новая схема просто «заимствует» два алгоритма из S без дальнейших изменений . Эти два алгоритма будут алгоритмами генерации ключа и подписи проверки Итак, две трети нашей задачи по разработке новой схемы уже выполнены. Таким образом, каждый новый элемент, появившийся в , появится в алгоритме подписи . Как и все алгоритмы подписи, этот алгоритм использует секретный ключ подписи и некоторое сообщение, которое нужно подписать. Он выведет подпись. На самом высоком уровне наш новый алгоритм подписи будет иметь два подварианта, выбранных ветвью, которая зависит от подписываемого входного сообщения. Эти два случая задаются следующим образом: «Нормальный» случай: для большинства сообщений M алгоритм подписи просто запускает исходный алгоритм подписи из оригинальной (безопасной) схемы S . «Злой» случай: для подмножества сообщений (разумного размера), которые имеют другую (и очень специфическую) форму, наш алгоритм подписи не будет выводить подпись. Вместо этого он выводит секретный ключ для всей схемы подписи. Это результат, который криптографы иногда называют «очень, очень плохим». Пока что это описание скрывает все действительно важные детали, но, по крайней мере, дает нам представление о том, куда мы пытаемся двигаться. Напомним, что в соответствии с определением UF-CMA, которое я описал выше, злоумышленнику разрешено запрашивать подписи для произвольных сообщений. Когда мы рассматриваем возможность использования этого определения с нашим модифицированным алгоритмом подписи, легко увидеть, что наличие этих двух случаев может сделать вещи захватывающими. В частности: если какой-либо злоумышленник может создать сообщение, которое запускает «злой» случай, его запрос на подпись сообщения фактически приведет к тому, что он получит секретный ключ схемы . Единственный способ, которым эта схема могла бы быть доказана в безопасности, это если бы мы могли как-то исключить «злое» дело вообще. Более конкретно: мы должны показать, что ни один злоумышленник не может создать сообщение, которое запускает «злой случай», или, по крайней мере, что их вероятность появления такого сообщения очень и очень мала (незначительна). Если бы мы могли это доказать, то наша схема в основном сводилась бы к исходной схеме безопасности . Что означает, что наша новая схема будет безопасной. Короче говоря, мы встроили в нашу новую схему нечто вроде бэкдора «мастер-пароль». Сообщение, нарушающее схему, конечно, вовсе не пароль. Поскольку это компьютерная наука, и нет ничего простого, сообщение на самом деле будет компьютерной программой . Мы назовем это P. Более конкретно, это будет своего рода программа, которая может быть декодирована в рамках нашего нового алгоритма подписи, а затем оценена (на некоторых входных данных) интерпретатором, который мы также поместим в этот алгоритм. Если говорить об этом формально, мы бы сказали, что сообщение содержит кодировку программы для универсальной машины Тьюринга (UTM), а также целое число в унарной кодировке t , представляющее количество временных шагов, которые машина должна быть разрешено работать. Тем не менее, я совершенно согласен, если вы предпочитаете думать о сообщении как о фрагменте Javascript, большом двоичном объекте виртуальной машины Ethereum в сочетании с некоторым максимальным значением «газа» для запуска, кодировке . Что действительно важно, так это функционирование программы P . Программа P , которая успешно инициирует «критический случай», содержит эффективную (например, полиномиальную) реализацию хеш-функции. И не просто любая хэш-функция. Чтобы действительно активировать черный ход, алгоритм P должен иметь функцию, идентичную или, по крайней мере, очень похожую на функцию случайного оракула H . Алгоритм подписи может проверить это сходство несколькими способами. Статья MRH дает очень элегантный вариант, о котором я расскажу ниже. Но для целей этой непосредственной интуиции давайте предположим, что наш алгоритм подписи проверяет это сходство вероятностно . В частности: чтобы убедиться, что P соответствует H, он не будет проверять соответствие при каждом возможном входе. Например, можно просто проверить, что P (x) = H (x) для некоторого большого (но полиномиального) числа случайных входных значений x. Итак, это черный ход. Давайте вкратце подумаем о том, что это означает для безопасности как внутри, так и вне режима случайного оракула. Напомним, что в модели случайного оракула «хэш-функция» H моделируется как случайная функция . На самом деле ни у кого в протоколе нет копии этой функции, у них просто есть доступ к третьей стороне («случайному оракулу»), которая может оценить ее для них. Если злоумышленник захочет запустить «злой случай» в нашей схеме подписи, ему каким-то образом нужно будет загрузить описание случайной функции из оракула. затем закодируйте его в программу P и отправьте подписывающему оракулу. Это кажется принципиально сложным. Чтобы сделать это точно — то есть, чтобы P соответствовало H при каждом вводе — злоумышленник должен запросить у случайного оракула каждый возможный ввод, а затем разработать программу P , которая кодирует все эти результаты. Конечно, злоумышленник может попытаться обмануть: создать небольшую функцию P , которая соответствует только H на небольшом количестве входных данных, и надеяться, что подписывающий не заметит. Тем не менее, даже это кажется довольно сложным, чтобы избежать наказания. Например, чтобы выполнить вероятностную проверку, алгоритм подписи может просто проверить, что P (x) = H (x) для большого количества случайных входных точек x. Этот подход позволит поймать мошенника с очень высокой вероятностью. (В конечном итоге мы воспользуемся чуть более элегантным подходом к проверке функции и обсудим этот момент ниже. Вышеизложенное едва ли можно назвать исчерпывающим анализом безопасности. Но на высоком уровне наш аргумент теперь должен быть ясен: в модели случайного оракула схема безопасна, потому что злоумышленник не может знать достаточно короткий «пароль» бэкдора, который взломает схему. Устранив «злой случай», схема просто деградирует к исходной, защищенной схеме S . В реальном мире мы не используем случайных оракулов. Когда мы хотим реализовать схему, которая имеет доказательство в ПЗУ, мы должны сначала «создать экземпляр» схемы, подставив какую-нибудь реальную хеш-функцию вместо случайного оракула H. . по определению быть эффективным оценивать и описывать. Это неявно означает, что он обладает описанием полиномиального размера и может быть оценен за ожидаемое полиномиальное время. Если бы мы этого не требовали, наши схемы никогда бы не сработали. С учетом этих фактов проблема с нашей новой схемой подписи становится очевидной. В этом параметре злоумышленник фактически имеет доступ к короткой эффективной программе P , которая соответствует хеш-функции H . На практике эта функция, вероятно, будет чем-то вроде SHA2 или Blake2. Но даже в странном случае, когда это какая-то сумасшедшая запутанная функция , злоумышленник все равно должен иметь программу, которую он может эффективно оценить. Поскольку у злоумышленника есть эта программа, он может легко закодировать ее в достаточно короткое сообщение и отправить подписывающему оракулу. Когда алгоритм подписи получит эту программу, он выполнит своего рода тест этой функции P против своей реализации H , и — когда он неизбежно найдет совпадение между двумя функциями с высокой вероятностью — он вывести секретный ключ схемы. Следовательно, в реальном мире наша схема всегда и навсегда полностью нарушена. Если вас устраивает неточная техническая интуиция, которую я изложил выше, не стесняйтесь пропустить этот раздел. Вы можете перейти к следующей части, которая пытается решить сложные философские вопросы, такие как « что это значит для случайного оракула модели » и « я думаю это все ерунда » и « почему мы ездим по бульвару, а паркуемся на подъездной дорожке? » Все, что я собираюсь сделать, это уточнить несколько технических деталей. Одна из самых больших частей, которая отсутствует в приведенной выше интуиции, — это спецификация того, как алгоритм подписи проверяет, что программа P , которую он получает от злоумышленника, действительно «соответствует» функции случайного оракула H. Очевидный способ состоит в том, чтобы просто оценить P( x ) = H( x ) для каждого возможного входа x и вывести секретный ключ схемы, если каждое сравнение будет успешным. В документе MRH предлагается очень изящный альтернативный способ решения этой проблемы. Предлагают протестировать функции на нескольких входных значений , причем даже не случайных. Более конкретно, они предлагают проверить, что P( x ) = H( x ) для значений с особым требованием, чтобы q было целым числом таким, что . Здесь представляет собой длину кодирования программы P в битах, а k — регулируемый параметр защиты схемы (например, k =128). Это означает, что для запуска бэкдора злоумышленник должен придумать программу P , которая может быть описана некоторым количеством битов (назовем ее n ) и при этом сможет правильно сопоставить выходные данные H с , например, q=2 n +128 различных входных точек. Если функция H является реальной хеш-функцией, такой как SHA256, то злоумышленнику должно быть достаточно легко найти некоторые n- битовая программа, которая соответствует H , скажем, q = 2 n +128 различных точек. Например, вот реализация SHA256 на Javascript, которая занимает менее 8192 бит. Если мы встроим интерпретатор Javascript в наш алгоритм подписи, то ему просто нужно оценить данную программу на q = 2(8,192)+128 = 16 512 различных входных точек, сравнить каждый результат с его собственной копией SHA256, и если они все совпадает, выведите секретный ключ. Однако, если H — это случайный оракул, злоумышленнику гораздо сложнее его использовать. Результатом оценки случайного оракула в q различных точек должна быть случайная строка длиной (как минимум) q бит. Несмотря на то, что вы, возможно, видели в Силиконовой долине ( NSFW ), алгоритмы сжатия не могут с высокой вероятностью сжимать случайные строки так сильно. В самом деле, для данной строки битов это настолько маловероятно, что атакующий преуспевает с вероятностью, которая в лучшем случае пренебрежимо мала в параметре безопасности схемы 9.1218 к . Это эффективно нейтрализует черный ход, когда H является случайным оракулом. Фух. Судя по действиям, а не словам, мнения криптографов мира по этому вопросу во многом разделились. Криптографы-теоретики , со своей стороны, мягко посмеивались над глупыми практиками, которые надеялись использовать случайные функции в качестве хеш-функций. Смахнув пепел со своих лацканов, они вернулись к более важным задачам, таким как поиск способов избавиться от криптографической обфускации. Прикладные академические криптографы с радостью приветствовали новые результаты и быстро написали 10 000 новых статей, каждая из которых нашла какой-то новый способ удалить случайные оракулы из существующей конструкции, в то же время делая указанную конструкцию значительно медленнее. более сложными и/или основанными на совершенно новых выдуманных и надуманных теоретико-числовых предположениях. (Исходя из личного опыта, это было прекрасное время.) Практикующие продолжал доверять модели случайного оракула. Ведь действительно, , почему не ? И, если честно, спорить с практиками по этому поводу довольно сложно. Это потому, что очень разумная точка зрения состоит в том, что эти «контрпримеры» смешны и искусственны. Ладно, я просто хороший. Они полная чушь, если честно. Никто никогда не разработает схему, которая выглядит так нелепо. В частности, вам нужна схема, которая явно анализирует ввод как программу, запускает эту программу, а затем проверяет, соответствует ли вывод программы другой хеш-функции. Какой протокол реального мира может сделать такую глупость? Разве мы не можем все еще доверять модели случайного оракула для схем, что не являются такими глупыми? Ну, может быть, а может и нет. Один простой ответ на этот аргумент состоит в том, что есть примеры менее искусственных схем, которые все же имеют случайные проблемы с оракулом. Но даже если считать эти результаты искусственными — факт остается фактом: пока мы знаем только о случайных контрпримерах оракулов, которые кажутся искусственными, у нас нет принципиального способа доказать, что вредность повлияет только на «искусственно выглядящие» протоколы. На самом деле, в любой момент кто-то может случайно (или намеренно) предложить совершенно «нормально выглядящую» схему, которая проходит проверку в модели случайного оракула, а затем разлетается на куски, когда ее фактически развертывают со стандартной хеш-функцией. К этому моменту схема может питать нашу инфраструктуру центра сертификации, или Биткойн, или наши системы ядерного оружия (если хотите быть драматичным).0005 Вероятность того, что это произойдет случайно, кажется низкой, но она становится выше по мере усложнения развернутых криптографических схем. Например, люди в Google сейчас начинают развертывать сложные многосторонние вычисления, а другие запускают протоколы с нулевым разглашением, которые на самом деле способны запускать (или подтверждать выполнение) произвольные программы криптографическим способом. В конечном счете, это странная и разочаровывающая ситуация, и, честно говоря, я ожидаю, что все закончится плачевно. Фото пользователя Flickr joyosity. Примечания: * Интуитивно это определение очень похоже на «псевдослучайность». Псевдослучайные функции должны быть неотличимы от случайных функций только в условиях, когда злоумышленник не знает какой-то «секретный ключ», используемый для этой функции. В то время как хеш-функции часто используются в протоколах, где нет возможности использовать секретный ключ, например, в протоколах шифрования с открытым ключом. ** Особая надежда заключалась в том, что мы сможем найти способ запутать семейств псевдослучайных функций (PRF). Идея заключалась бы в том, чтобы обернуть PRF с ключом, который мог бы оценить любой, даже если он на самом деле не знал ключа. *** Может показаться, что «предположим, что существует схема защищенной подписи» — это дополнительное предположение. Однако: если мы собираемся делать заявления в модели случайного оракула оказывается, что дополнительных допущений нет. Это связано с тем, что в ПЗУ у нас есть доступ к «защищенной» (по крайней мере, устойчивой к коллизиям, устойчивой к [второму] предварительному изображению) хеш-функции, что означает, что мы можем создавать подписи на основе хэшей. Таким образом, в модели случайного оракула существование схем подписи предоставляется «бесплатно». **** Оговорка «за исключением незначительной вероятности [в регулируемом параметре безопасности схемы]» важна по двум причинам. Во-первых, целеустремленный злоумышленник всегда может попытаться подделать подпись, просто угадывая значения по одному, пока не получит то, что удовлетворяет алгоритму проверки. Если атакующий может бежать неограниченное количество временных шагов, он всегда в конце концов выигрывает эту игру. Мэтью Гринин, основы, доказуемая безопасность, без категорий В качестве проверки концепции мы провели атаку в нашей лаборатории на вымышленный веб-сайт и жертву (чтобы не нанести вред реальным системам).
В нашей демонстрации жертва использует Internet Explorer, и мы показываем, как злоумышленник может завладеть учетной записью жертвы.
это первый раз слабые места в RC4 при использовании в TLS и HTTPS эксплуатируются против реальных устройств . Чтобы успешно расшифровать 16-символьный файл cookie с вероятностью успеха 94%, необходимо зафиксировать примерно 9⋅2 27 шифровок файла cookie.
Поскольку мы можем заставить клиента передавать 4450 запросов в секунду, это количество можно собрать всего за 75 часов.
Если злоумышленнику повезет, потребуется захватить меньше шифров.
В нашей демонстрации для выполнения атаки хватило 52 часов, после чего 6,2⋅2 27 запросов было перехвачено.
Генерацию этих запросов можно даже растянуть во времени: их не нужно захватывать все сразу.
На последнем этапе атаки перехваченные запросы преобразуются в список из 2 23 вероятных значений cookie.
Все файлы cookie в этом списке можно протестировать менее чем за 7 минут. Наша атака не ограничивается расшифровкой файлов cookie .
Любые данные или информация, которые неоднократно шифровались, могут быть восстановлены. Наш исследовательский документ, стоящий за атакой, называется «Все ваши предубеждения принадлежат нам: взлом RC4 в WPA-TKIP и TLS».
В статье представлены атаки не только на TLS/HTTPS, но и на WPA-TKIP.
Наша атака на WPA-TKIP выполняется всего за час и позволяет злоумышленнику внедрить и расшифровать произвольные пакеты. На этой странице мы сосредоточились на HTTPS, потому что он используется чаще, чем WPA-TKIP.
Документ был представлен на USENIX Security 2015, и вы можете просмотреть слайды онлайн. Мы также хотели бы отметить, что существует независимый перевод нашей статьи на испанский язык. По оценкам, первая атака на RC4, используемую в TLS, заняла более 2000 часов.
Для его расшифровки требовалось 13⋅2 30 шифрований файла cookie, и жертва могла генерировать 1700 запросов в секунду (каждый запрос содержал зашифрованный файл cookie). Атака Bar Mitzvah опирается на потоки ключей с предсказуемыми младшими битами, которые происходят один раз каждые 2 24 соединений.
Известно, что только первые 100 байтов ключевого потока являются слабыми.
Однако в настоящее время неизвестны системы, которые шифруют конфиденциальные данные в этих позициях. Еще одна атака нацелена на пароли, зашифрованные с помощью RC4, и основана на статистической погрешности в начальных байтах ключевого потока.
Для его расшифровки требуется примерно 2 26 шифрований пароля.
Однако создание большого количества запросов в этом сценарии оказывается затруднительным, поскольку каждый запрос должен выполняться в новом соединении TLS. Наша работа значительно сокращает время выполнения атаки, и мы считаем это улучшение очень тревожным.
Учитывая, что по-прежнему существуют неиспользованные предубеждения, что можно реализовать более эффективные алгоритмы и изучить лучшие методы генерации трафика, мы ожидаем дальнейших улучшений в будущем. Он основан на двух типах статистических погрешностей, присутствующих в ключевом потоке.
Первый заключается в том, что два последовательных байта смещены в сторону определенных значений.
Их обычно называют предубеждениями Флюрера-МакГрю.
Второй тип смещений заключается в том, что пара последовательных байтов может повторяться.
Они называются предубеждениями ABSAB Мантина.
В нашей атаке сочетаются оба типа предубеждений. Эти предубеждения позволяют нам расшифровывать повторяющихся открытых текстов, таких как файлы cookie. Единственная хорошая контрмера — прекратить использование RC4.
Тем не менее, мы заметили, что создание необходимого объема трафика может быть узким местом при выполнении атаки.
Следовательно, атаки можно сделать более дорогими, но не предотвратить, затруднив генерацию трафика.
Один из вариантов — запретить браузерам создавать параллельные соединения при использовании RC4 (обычно для более быстрой загрузки веб-сайтов создаются несколько соединений).
Это снижает скорость, с которой клиенты могут выполнять запросы, а значит, они медленнее генерируют трафик.
Однако подчеркнем, что это лишь увеличит время выполнения атак, а не предотвратит их. Да. Мы можем взломать сеть WPA-TKIP в течение часа.
Точнее, после успешного выполнения атаки злоумышленник может расшифровать и внедрить произвольные пакеты, отправленные клиенту. Более подробные версии нескольких графиков представлены в нашей статье: Несмотря на то, что полная статистика ключевого потока слишком велика, чтобы ее можно было разместить в Интернете, мы предоставляем наборы данных по большинству обнаруженных нами предубеждений: Наконец, вы также можете загрузить нашу R-реализацию М-теста Фукса и Кенетта. Creative Commons Attribution 4.0 Международная лицензия | Дизайн вдохновлен TEMPLATED. Уровень бесплатного пользования KMS доступен в регионе Amazon Web Services China (Ningxia) под управлением NWCD и в регионе Amazon Web Services China (Пекин) под управлением Sinnet. Уровень бесплатного пользования включает 20 000 бесплатных запросов в месяц. Подробнее » Каждый мастер-ключ клиента (CMK), который вы создаете в Amazon Key Management Service (KMS), стоит 6,88 йен в месяц до тех пор, пока вы не удалите его, независимо от того, где находился базовый материал ключа. Плата не взимается за следующее: Стоимость каждого запроса API к службе управления ключами Amazon: Все регионы Китая: 1 CMK используется в качестве ключа KMS, управляемого клиентом, при создании 2500 зашифрованных томов EBS в месяц с помощью CLI или API Amazon KMS. Стоимость Размеры: 1 CMK используется для шифрования 10 000 уникальных файлов, которые совместно расшифровываются для доступа 2 000 000 раз в месяц. Стоимость Размеры: 1 ECC 256 CMK используется для подписи 100 000 файлов через CLI или API Amazon KMS. Стоимость Размеры: Если вы включите Amazon CloudTrail в своей учетной записи, вы сможете получать журналы вызовов API, сделанных Amazon KMS или отправленных им. Дополнительную информацию см. на странице цен на Amazon CloudTrail. Узнайте, как начать работу Найдите ссылки на наше руководство для разработчиков, полезные видеоролики и руководства по работе с консолью. В случае активного противника (который может заставить игроков произвольно отклоняться от протокола) необходимо, чтобы, если все комбинации t+1 игроков расшифровывали сообщение, должно быть большинство комбинаций t+1 игроков. без коррумпированных игроков. Это дает нам, что t
В случае активного противника (который может заставить игроков произвольно отклоняться от протокола) необходимо, чтобы, если все комбинации t+1 игроков расшифровывали сообщение, должно быть большинство комбинаций t+1 игроков. без коррумпированных игроков. Это дает нам, что t Пусть CC=Commit(s˚C,e˚C,KNHCs,KNHCe,KHC′,aEC′) вызов, выводимый A, первый шаг взаимодействия в протоколе 2, как мы можем видеть в таблице 3. Тогда претендент выбирает b ←${0,1} и действует следующим образом:
Пусть CC=Commit(s˚C,e˚C,KNHCs,KNHCe,KHC′,aEC′) вызов, выводимый A, первый шаг взаимодействия в протоколе 2, как мы можем видеть в таблице 3. Тогда претендент выбирает b ←${0,1} и действует следующим образом: С помощью этой информации претендент может вычислить sB вклад честных игроков в s так, что s=sC+sB. Вычислив эти значения, претендент следует протоколу.
С помощью этой информации претендент может вычислить sB вклад честных игроков в s так, что s=sC+sB. Вычислив эти значения, претендент следует протоколу.
 Чтобы убедиться в этом, мы воспользуемся безопасностью обмена секретами Шамира, поскольку противник может контролировать не более t игроков. Таким образом, общая стоимость полностью не определяется долями коррумпированных игроков, поэтому оба случая (b=0 и b=1) неразличимы для противника.
Чтобы убедиться в этом, мы воспользуемся безопасностью обмена секретами Шамира, поскольку противник может контролировать не более t игроков. Таким образом, общая стоимость полностью не определяется долями коррумпированных игроков, поэтому оба случая (b=0 и b=1) неразличимы для противника. 6. Реализация
 Чтобы проверить это, мы воспользуемся ограничениями на ξ в лемме 1 и оценкой твердости LWE, данной Albrecht et al. в [19]. Мы используем оценщик LWE, потому что, насколько нам известно, не известно ни о каких серьезных атаках, использующих определенные свойства R-LWE, поэтому расчетная сложность для LWE переводится как расчетная сложность для R-LWE.
Чтобы проверить это, мы воспользуемся ограничениями на ξ в лемме 1 и оценкой твердости LWE, данной Albrecht et al. в [19]. Мы используем оценщик LWE, потому что, насколько нам известно, не известно ни о каких серьезных атаках, использующих определенные свойства R-LWE, поэтому расчетная сложность для LWE переводится как расчетная сложность для R-LWE. 6.1. Выбор параметров

6.
 2. Подробности реализации
2. Подробности реализации Это основная причина, по которой мы взяли q простым, так как ни одно из сокращений не требует этого. .
Это основная причина, по которой мы взяли q простым, так как ни одно из сокращений не требует этого. . А учитывая, что не нужно устанавливать никакое другое значение, которое злоумышленник не может использовать (поскольку противник становится неактуальным), схема обязательств на любом последующем этапе коммуникации кажется ненужной. Тем не менее, эти этапы фиксации могут быть добавлены без каких-либо существенных изменений в протоколе или подтверждения безопасности или правильности, только с немного более медленным выполнением.
А учитывая, что не нужно устанавливать никакое другое значение, которое злоумышленник не может использовать (поскольку противник становится неактуальным), схема обязательств на любом последующем этапе коммуникации кажется ненужной. Тем не менее, эти этапы фиксации могут быть добавлены без каких-либо существенных изменений в протоколе или подтверждения безопасности или правильности, только с немного более медленным выполнением. 6.3. Результаты моделирования
 Также стоит упомянуть, что любой результат, который мы получаем от выполнения моделирования, был получен путем усреднения времени 10 000 выполнений кода, чтобы лучше отобразить результаты, избавившись от выбросов.
Также стоит упомянуть, что любой результат, который мы получаем от выполнения моделирования, был получен путем усреднения времени 10 000 выполнений кода, чтобы лучше отобразить результаты, избавившись от выбросов. Это означает, что зависимость должна быть приблизительно экспоненциальной в активном случае, когда u=3t+1, и приблизительно линейной в пассивном случае, когда u=t+1. При получении результатов моделирования мы собрали результаты для значений t, наиболее часто используемых в реальных приложениях, таких как электронное голосование, что означает t<3 для активных противников и t<7 для пассивных противников. Это решение в основном связано с тем, как мы реализовали симуляцию, поскольку вместо того, чтобы протоколы нескольких игроков выполнялись одновременно, мы выполняем их последовательно, а затем берем максимальное затраченное время как общее время. В случае с генерацией ключей, поскольку существуют различные этапы взаимодействия, этот процесс применяется к каждому из них. Поэтому из-за нехватки времени мы были ограничены в том, сколько игроков мы могли симулировать в протоколах при запуске 10 000 запусков кодов. Сказав все это, результаты, которые мы получили для зависимости от t, соответствовали нашим предсказаниям.
Это означает, что зависимость должна быть приблизительно экспоненциальной в активном случае, когда u=3t+1, и приблизительно линейной в пассивном случае, когда u=t+1. При получении результатов моделирования мы собрали результаты для значений t, наиболее часто используемых в реальных приложениях, таких как электронное голосование, что означает t<3 для активных противников и t<7 для пассивных противников. Это решение в основном связано с тем, как мы реализовали симуляцию, поскольку вместо того, чтобы протоколы нескольких игроков выполнялись одновременно, мы выполняем их последовательно, а затем берем максимальное затраченное время как общее время. В случае с генерацией ключей, поскольку существуют различные этапы взаимодействия, этот процесс применяется к каждому из них. Поэтому из-за нехватки времени мы были ограничены в том, сколько игроков мы могли симулировать в протоколах при запуске 10 000 запусков кодов. Сказав все это, результаты, которые мы получили для зависимости от t, соответствовали нашим предсказаниям. В активном случае они вели себя более чем линейно в трех имевшихся у нас точках, а в пассивном — примерно линейно. Более глубокий анализ невозможен без сбора более обширных данных.
В активном случае они вели себя более чем линейно в трех имевшихся у нас точках, а в пассивном — примерно линейно. Более глубокий анализ невозможен без сбора более обширных данных. Как видно из Таблицы 6, время генерации ключа значительно меньше, чем время расшифровки, в 4-7 раз медленнее. Это, однако, не представляет большой проблемы, так как по замыслу в большинстве реализаций один этап генерации ключа будет использоваться для расшифровки многих сообщений; поэтому мы можем сосредоточить наш основной анализ на времени расшифровки. На этом фронте 530,36 мс на дешифрование в активном случае переводятся примерно в 7000 сообщений в час, а 131,73 мс на сообщение в пассивном случае переводятся примерно в 27000 сообщений в час. Как мы видим, это будет половина этих голосов в час при n=819.2, которые понадобятся против активного противника, как мы сказали в разделе 6.1.
Как видно из Таблицы 6, время генерации ключа значительно меньше, чем время расшифровки, в 4-7 раз медленнее. Это, однако, не представляет большой проблемы, так как по замыслу в большинстве реализаций один этап генерации ключа будет использоваться для расшифровки многих сообщений; поэтому мы можем сосредоточить наш основной анализ на времени расшифровки. На этом фронте 530,36 мс на дешифрование в активном случае переводятся примерно в 7000 сообщений в час, а 131,73 мс на сообщение в пассивном случае переводятся примерно в 27000 сообщений в час. Как мы видим, это будет половина этих голосов в час при n=819.2, которые понадобятся против активного противника, как мы сказали в разделе 6.1. 7. Выводы и будущая работа
 , что нежелательно. Если бы для неинтерактивного совместного использования значения шума использовались другие методы, этого можно было бы избежать. Во-вторых, и это более характерно для структуры наших протоколов, это тот факт, что использование заглушения шума само по себе приводит к тому, что наша реализация использует очень большие размеры для решеток. Это связано с тем, что для гарантии статистической неразличимости нам нужно, чтобы шум был экспоненциально больше, чем секрет, в то время как схема шифрования LPR требует, чтобы шум был меньше, чем q4, а это означает, что параметр ξ пропорционально очень мал по сравнению с модулем q . Затем это влияет на размер решетки, необходимой для обеспечения того, чтобы конкретный экземпляр проблемы R-LWE имел желаемое количество битов безопасности. Этого ограничения можно было бы избежать, только используя способ обеспечения безопасности, отличный от шумового утопления, что является ключевым элементом нашего предложения.
, что нежелательно. Если бы для неинтерактивного совместного использования значения шума использовались другие методы, этого можно было бы избежать. Во-вторых, и это более характерно для структуры наших протоколов, это тот факт, что использование заглушения шума само по себе приводит к тому, что наша реализация использует очень большие размеры для решеток. Это связано с тем, что для гарантии статистической неразличимости нам нужно, чтобы шум был экспоненциально больше, чем секрет, в то время как схема шифрования LPR требует, чтобы шум был меньше, чем q4, а это означает, что параметр ξ пропорционально очень мал по сравнению с модулем q . Затем это влияет на размер решетки, необходимой для обеспечения того, чтобы конкретный экземпляр проблемы R-LWE имел желаемое количество битов безопасности. Этого ограничения можно было бы избежать, только используя способ обеспечения безопасности, отличный от шумового утопления, что является ключевым элементом нашего предложения. Таким образом, коды должны быть тщательно проанализированы, чтобы гарантировать вычислительную безопасность (например, некоторые из случайных выборок на самом деле нельзя отличить от равномерно случайных) и что никакие другие атаки на основе реализации (например, атаки по сторонним каналам) не могут быть выполнены. Кроме того, для любого важного практического применения коды должны быть оптимизированы по эффективности.
Таким образом, коды должны быть тщательно проанализированы, чтобы гарантировать вычислительную безопасность (например, некоторые из случайных выборок на самом деле нельзя отличить от равномерно случайных) и что никакие другие атаки на основе реализации (например, атаки по сторонним каналам) не могут быть выполнены. Кроме того, для любого важного практического применения коды должны быть оптимизированы по эффективности. Это открывает доступ к совершенно новому набору возможностей для приложений.
Это открывает доступ к совершенно новому набору возможностей для приложений. Вклад авторов
Финансирование
Заявление Институционального контрольного совета
Заявление об информированном согласии

Заявление о доступности данных
Конфликт интересов
Сокращения
CPA Chosen Plaintext Attack GAPSVP GAP Shortest Vector Problem HMAC Hash-based Message Authentication Code K-DGS Discrete Gaussian Sampling over K LWE Learning with Errors NIST National Institute of Standards and Technology NIVSS Non-Interactive Verifiable Secret Sharing R-LWE Ring Learning with Errors PRF Псевдослучайная функция PRSS Псевдослучайный обмен секретами TTP Доверенная третья сторона  Поскольку произведение в Rq выполняется через антициклическую матрицу, мы знаем, что
Поскольку произведение в Rq выполняется через антициклическую матрицу, мы знаем, что Однако в протоколе всякий раз, когда проверка не проходит, протокол останавливается. Чтобы справиться с этим, мы реализуем следующую политику разрешения споров, когда спор возникает всякий раз, когда игрок получает значение, которое не проходит проверку, с указанием того, какой другой игрок отправил значения.
Однако в протоколе всякий раз, когда проверка не проходит, протокол останавливается. Чтобы справиться с этим, мы реализуем следующую политику разрешения споров, когда спор возникает всякий раз, когда игрок получает значение, которое не проходит проверку, с указанием того, какой другой игрок отправил значения. Наконец, обратите внимание, что, поскольку в каждом споре участвует не более одного честного игрока, доля коррумпированных игроков никогда не превысит u3.
Наконец, обратите внимание, что, поскольку в каждом споре участвует не более одного честного игрока, доля коррумпированных игроков никогда не превысит u3. Приложение А.2. Безопасность


 Вычислив эти значения, претендент приступает к протоколу.
Вычислив эти значения, претендент приступает к протоколу. □
□ Приложение Б. Доказательства вспомогательных теорем и лемм
Приложение Б.1. Доказательство теоремы 2

 Это означает, что с немалой вероятностью B может решить решающую задачу R-LWEχ так, как мы хотели.
Это означает, что с немалой вероятностью B может решить решающую задачу R-LWEχ так, как мы хотели. Это означает, что с непренебрежимо малой вероятностью B может решить проблему принятия решений R-LWEχ так, как мы хотели, поскольку можно с непренебрежимо малой вероятностью отличить незначительное событие от непренебрежимо малого события. □ 9, мы знаем оценку для Ψ¯. Учитывая этот результат, теперь мы можем связать распределения, используя тот факт, что Ω является округленным гауссовым уравнением и неравенством Милля:
Это означает, что с непренебрежимо малой вероятностью B может решить проблему принятия решений R-LWEχ так, как мы хотели, поскольку можно с непренебрежимо малой вероятностью отличить незначительное событие от непренебрежимо малого события. □ 9, мы знаем оценку для Ψ¯. Учитывая этот результат, теперь мы можем связать распределения, используя тот факт, что Ω является округленным гауссовым уравнением и неравенством Милля: Приложение C. Ссылка на репозиторий
Ссылки
 ; стр. 659–690. [Google Scholar]
; стр. 659–690. [Google Scholar] Схема порогового шифрования. Будущий генерал. вычисл. Сист. 2014 , 36, 180–186. [Google Scholar] [CrossRef]
Схема порогового шифрования. Будущий генерал. вычисл. Сист. 2014 , 36, 180–186. [Google Scholar] [CrossRef] В материалах конференции по теории криптографии, Кембридж, Массачусетс, США, 10–12 февраля 2005 г.; стр. 342–362. [Академия Google]
В материалах конференции по теории криптографии, Кембридж, Массачусетс, США, 10–12 февраля 2005 г.; стр. 342–362. [Академия Google] Предложение Задача о решетке Генерация ключей Реализация [6] LWE ✓ ✗ [7] LWE ✗ ✗ [8] LWE ✓ ✗ [5] LWE ✗ ✗ [9] R-LWE ✗ ✗ Our proposal R-LWE ✓ ✓ 
Протокол расшифровки Входы: sj, KH s.t. j∉h, φ · (·), FH Игрок PJ ° (U, V) e˜j=v−sj·u →xj+e˜j Key Generation Protocol Inputs: χ, Φ·KG(·), μ Player Pj sj,ej←χKHj,KNHjs, KNHje ←$Zq∀|H|=n−ts˚j=sj−∑HΦKNHjsKG(μ)e˚j=ej−∑HΦKNHjeKG(μ)aEj ←$RqKHj′,aEj′=Shamir.  Shares(KHj,aEj) Cj=Commit(s˚j,e˚j,KNHjs,KNHje,KHj′,aEj′)
Shares(KHj,aEj) Cj=Commit(s˚j,e˚j,KNHjs,KNHje,KHj′,aEj′) →Cj ←Ckk=1u →s˚j,e˚j,KNHjs,KNHje,KHj′,aEj′ ←s˚k,e˚k,KNHks,KNHke,KHk′,aEk′k=1u Verify(Ck)j={‘принять’или’отклонить’}k=1u → Verify(Ck)jk=1u ← Verify(Ci)ki,k=1u if Verify(Ci)k= ‘отклонить’ для некоторого i,k прерывание Verify.  interval(s˚k)j={‘принять’или’отклонить’}k=1uVerify.interval(e˚k)j={‘принять’или’отклонить’}k=1usj= ∑k=1us˚k+∑H∌PjΦKNHjsKG(μ)·fH(j)ej=∑k=1ue˚k+∑H∌PjΦKNHjeKG(μ)·fH(j)KHj=∑k=1uKHk′aEj=∑k= 1uaEk′
interval(s˚k)j={‘принять’или’отклонить’}k=1uVerify.interval(e˚k)j={‘принять’или’отклонить’}k=1usj= ∑k=1us˚k+∑H∌PjΦKNHjsKG(μ)·fH(j)ej=∑k=1ue˚k+∑H∌PjΦKNHjeKG(μ)·fH(j)KHj=∑k=1uKHk′aEj=∑k= 1uaEk′ →Провер.интервал(s˚k)j,Провер.интервал(e˚k)jk=1u .interval(e˚i)ki,k=1u if Verify.interval(s˚i)k= ‘отклонить’ для некоторого i,k прерывание , если проверить. Interval (Eвку) K = ‘Отказ для I, K ABORT → Aej, KHJTOKS.H∌.H∌P.H∌.H∌PK.H∌P.H∌.H∌P.H∌P.H∌.H∌P.H∌.H∌PK.HJT.HJS.H∌.H∌.HJTOKS. .  ,KHks.t.H∌Pjk=1u
,KHks.t.H∌Pjk=1u KH=Reconstruct.Shamir(KHk)s.t.H∌PjaE=Reconstruct.Shamir(aEk)bEj=aE·sj+ej →aE,bEj ←bEkk=1u bE=Reconstruct.Shamir(bEk) →bE n = 4096 q = 713,623,846,352,979,940,529,142,984,724,747,568,191,373,381 κ = 168 ξ = 14.  8978610
8978610 ID = 8,403,614,205,785,368,527,542,540,898,258,331,059,093,504 IKG = 872,305,872,233,851,041,593,123,383,308,976,128 Bits of Security = 121 Operating System Ubuntu 18.04.5 LTS CPU Intel® Core™ i5-8500 Memory 15.  4 GiB
4 GiB Word Size 64 bits Тактовая частота процессора 3,00 ГГц n Key Generation Decryption Encryption Active Passive Active Passive 4096 7031.  34 ms
34 ms 1005.63 ms 530.36 ms 131,73 мс 191,79 мс 8192 14320,01 MS 2160,05 MS 967.24S 6156565656565656565656565656565656565656565656565615656565656565656569н.0655 539,71 мс
© 2022 авторами. Лицензиат MDPI, Базель, Швейцария. Эта статья находится в открытом доступе и распространяется на условиях лицензии Creative Commons Attribution (CC BY) (https://creativecommons.org/licenses/by/4.0/). Что такое оптимизм? Использование накопительных пакетов для помощи в масштабировании Ethereum
Коротко

Что такое оптимизм?

 По данным Dune Analytics, по состоянию на март 2022 года Optimism обеспечивает около 740 миллионов долларов внутрисетевой стоимости по сравнению с чуть более 1 миллиарда долларов в январе.
По данным Dune Analytics, по состоянию на март 2022 года Optimism обеспечивает около 740 миллионов долларов внутрисетевой стоимости по сравнению с чуть более 1 миллиарда долларов в январе. Как работает Optimism

Что особенного в Оптимизме?

Как использовать Оптимизм
 Депозиты занимают около двадцати минут, и MetaMask указал нам комиссию в размере 18 долларов за перевод 1 ETH.
Депозиты занимают около двадцати минут, и MetaMask указал нам комиссию в размере 18 долларов за перевод 1 ETH. Будущее оптимизма

Будьте в курсе новостей криптовалюты, получайте ежедневные обновления на свой почтовый ящик.
Ваш адрес электронной почты Без рубрики – Несколько мыслей о криптографической инженерии
 Предыдущие посты смотрите здесь:
Предыдущие посты смотрите здесь:
Часть 2: Формализованное ПЗУ, схема и набросок доказательства
Часть 3: Как мы злоупотребляем ПЗУ, чтобы наши доказательства безопасности работали
Часть 4: Еще несколько примеров использования ПЗУ
 И это стало для меня главным источником сожаления, так как я всегда планировал пятый и последний пост , чтобы закрыть весь этот беспорядок. Это должно было стать лучшим из всех: то, что я хотел написать все это время.
И это стало для меня главным источником сожаления, так как я всегда планировал пятый и последний пост , чтобы закрыть весь этот беспорядок. Это должно было стать лучшим из всех: то, что я хотел написать все это время. К сожалению, конец близок. Подобно воображаемому городу, который Леонардо де Каприо исследовал в скучной части «Начала», модель случайного оракула рушится под тяжестью собственных противоречий.
К сожалению, конец близок. Подобно воображаемому городу, который Леонардо де Каприо исследовал в скучной части «Начала», модель случайного оракула рушится под тяжестью собственных противоречий. В котором мы (очень быстро) напоминаем читателю, что такое хеш-функции, что такое случайные функции и что такое случайный оракул.
 Мы часто обозначаем эти функции следующим образом:
Мы часто обозначаем эти функции следующим образом: В идеальном мире ваш протокол мог бы, например, случайным образом выбирать одну из огромного количества возможных функций при настройке, запекать идентификатор этой функции в открытый ключ или что-то в этом роде, и тогда все было бы хорошо. 9{256}}. Простое «запись» идентификатора выбранной вами функции потребует памяти, экспоненциально зависящей от входной длины функции. Поскольку мы хотим, чтобы наши криптографические алгоритмы были эффективными (имея в виду, несколько более формально, что они работают за полиномиальное время), использование случайных функций практически невозможно.
В идеальном мире ваш протокол мог бы, например, случайным образом выбирать одну из огромного количества возможных функций при настройке, запекать идентификатор этой функции в открытый ключ или что-то в этом роде, и тогда все было бы хорошо. 9{256}}. Простое «запись» идентификатора выбранной вами функции потребует памяти, экспоненциально зависящей от входной длины функции. Поскольку мы хотим, чтобы наши криптографические алгоритмы были эффективными (имея в виду, несколько более формально, что они работают за полиномиальное время), использование случайных функций практически невозможно.
 Модель справляется с этим просто: вместо того, чтобы давать отдельным участникам протокола описание самой хэш-функции — она слишком велика, чтобы с ней можно было иметь дело — они дают каждой стороне (включая противника) получают доступ к волшебному «оракулу», который может эффективно оценить случайную функцию H и передать им результат.
Модель справляется с этим просто: вместо того, чтобы давать отдельным участникам протокола описание самой хэш-функции — она слишком велика, чтобы с ней можно было иметь дело — они дают каждой стороне (включая противника) получают доступ к волшебному «оракулу», который может эффективно оценить случайную функцию H и передать им результат. Внутри этой искусственной модели мы получаем идеальные хэш-функции без каких-либо проблем.
Внутри этой искусственной модели мы получаем идеальные хэш-функции без каких-либо проблем. Это уже кажется довольно смешным…

 Но обычно эти сбои происходят из-за того, что сама хеш-функция явно сломана (как это произошло, когда MD4 и MD5 некоторое время назад сломались). Тем не менее, эти недостатки обычно исправляются простым переключением на лучшую функцию. Более того, исторически сложилось так, что практические атаки чаще происходят из-за очевидных недостатков, таких как обнаружение коллизий хэшей, искажающих схемы подписи, а не из-за какой-то экзотической математической ошибки. Что подводит нас к последнему критическому замечанию…
Но обычно эти сбои происходят из-за того, что сама хеш-функция явно сломана (как это произошло, когда MD4 и MD5 некоторое время назад сломались). Тем не менее, эти недостатки обычно исправляются простым переключением на лучшую функцию. Более того, исторически сложилось так, что практические атаки чаще происходят из-за очевидных недостатков, таких как обнаружение коллизий хэшей, искажающих схемы подписи, а не из-за какой-то экзотической математической ошибки. Что подводит нас к последнему критическому замечанию… **
** CGH98: «нереализуемая» схема98 Статья STOC Канетти, Гольдрейха и Халеви (далее CGH). Я собираюсь посвятить оставшуюся часть этого (длинного!) поста объяснению сути того, что они обнаружили.
 Совсем другое дело знать, что на практике существуют схемы, которые могут пройти мимо ваших доказательств, как Терминатор, проникший в Сопротивление, а затем взорваться на вас самым серьезным образом.
Совсем другое дело знать, что на практике существуют схемы, которые могут пройти мимо ваших доказательств, как Терминатор, проникший в Сопротивление, а затем взорваться на вас самым серьезным образом. Смысл этих конкретных контрпримеров в том, чтобы сделать нарочито искусственных вещей, дабы подчеркнуть проблемы с ПЗУ. Но это не значит, что «реалистично» выглядящие схемы не подойдут.
Смысл этих конкретных контрпримеров в том, чтобы сделать нарочито искусственных вещей, дабы подчеркнуть проблемы с ПЗУ. Но это не значит, что «реалистично» выглядящие схемы не подойдут. Схема подписи

 ****
**** Поскольку мы начали с (предполагаемой) безопасной схемы подписи 9 S , этот аргумент в основном сводится к тому, чтобы показать, что в модели случайного оракула странные дополнительные функции, которые мы добавили на предыдущем шаге, на самом деле не делают схему пригодной для эксплуатации.
Поскольку мы начали с (предполагаемой) безопасной схемы подписи 9 S , этот аргумент в основном сводится к тому, чтобы показать, что в модели случайного оракула странные дополнительные функции, которые мы добавили на предыдущем шаге, на самом деле не делают схему пригодной для эксплуатации. Построение сломанной схемы
 Эта схема включает в себя три упомянутых выше алгоритма: генерацию ключа, подпись и проверку.
Эта схема включает в себя три упомянутых выше алгоритма: генерацию ключа, подпись и проверку. Это выведет совершенно красивую подпись, которая, как мы можем ожидать, будет работать нормально.
Это выведет совершенно красивую подпись, которая, как мы можем ожидать, будет работать нормально. С этого момента она сможет подписать любое сообщение, которое захочет — что, очевидно, нарушает безопасность схемы UF-CMA. Если это слишком теоретически для вас: представьте, что вы запрашиваете подписанный сертификат у LetsEncrypt и вместо этого получаете копию ключей подписи LetsEncrypt. Теперь вы тоже являетесь центром сертификации. Именно такую ситуацию мы описываем.
С этого момента она сможет подписать любое сообщение, которое захочет — что, очевидно, нарушает безопасность схемы UF-CMA. Если это слишком теоретически для вас: представьте, что вы запрашиваете подписанный сертификат у LetsEncrypt и вместо этого получаете копию ключей подписи LetsEncrypt. Теперь вы тоже являетесь центром сертификации. Именно такую ситуацию мы описываем. Любой, кто знает пароль, может взломать схему. Теперь все зависит от того, сможет ли злоумышленник подобрать этот пароль.
Любой, кто знает пароль, может взломать схему. Теперь все зависит от того, сможет ли злоумышленник подобрать этот пароль. Так что же такое «черный ход»?
 tgz контейнера Docker или любом другом. исполняемый формат, который вам нравится.
tgz контейнера Docker или любом другом. исполняемый формат, который вам нравится.
Случай 1: в модели случайного оракула
 Достаточно сказать, что эта стратегия не будет практичной: для выполнения любого из них потребуется экспоненциальное количество времени, и размер P также будет экспоненциальным по входной длине функции. Таким образом, этот злоумышленник практически гарантированно потерпит неудачу.
Достаточно сказать, что эта стратегия не будет практичной: для выполнения любого из них потребуется экспоненциальное количество времени, и размер P также будет экспоненциальным по входной длине функции. Таким образом, этот злоумышленник практически гарантированно потерпит неудачу. )
) Случай 2: В «реальном мире»
 Более того, мы должны дополнительно предположить, что все стороны, включая злоумышленника, обладают описанием хеш-функции. Это стандартное предположение в криптографии и просто формулировка принципа Керкхоффа.
Более того, мы должны дополнительно предположить, что все стороны, включая злоумышленника, обладают описанием хеш-функции. Это стандартное предположение в криптографии и просто формулировка принципа Керкхоффа.
Несколько скучных технических подробностей (которые вы можете пропустить)
 Но выполнение этого исчерпывающего требует экспоненциального времени.
Но выполнение этого исчерпывающего требует экспоненциального времени. Если мы консервативно предположим, что H производит (как минимум) 1-битный дайджест, это означает, что мы фактически кодируем как минимум 2 n +128 бит данных в строку длиной n .
Если мы консервативно предположим, что H производит (как минимум) 1-битный дайджест, это означает, что мы фактически кодируем как минимум 2 n +128 бит данных в строку длиной n . Тем не менее, для того, чтобы бэкдор сработал, мы требуем, чтобы кодировка программы P была меньше половины размера . Поэтому вы можете представить себе процесс, с помощью которого злоумышленник сжимает случайную строку в эту программу 9.1278 P , чтобы быть очень эффективным алгоритмом сжатия, человек берет случайную строку и сжимает ее в строку меньше половины размера.
Тем не менее, для того, чтобы бэкдор сработал, мы требуем, чтобы кодировка программы P была меньше половины размера . Поэтому вы можете представить себе процесс, с помощью которого злоумышленник сжимает случайную строку в эту программу 9.1278 P , чтобы быть очень эффективным алгоритмом сжатия, человек берет случайную строку и сжимает ее в строку меньше половины размера. Так что же все это значит?


 На самом деле, понятие «искусственно выглядящий» в значительной степени является человеческим суждением, а не чем-то, что можно реально обдумать математически.
На самом деле, понятие «искусственно выглядящий» в значительной степени является человеческим суждением, а не чем-то, что можно реально обдумать математически. Мы не можем полностью исключить возможность того, что контрпримеры типа CGH и MRH могут быть на самом деле может случиться в этих странных условиях, если кто-то хоть немного небрежен.
Мы не можем полностью исключить возможность того, что контрпримеры типа CGH и MRH могут быть на самом деле может случиться в этих странных условиях, если кто-то хоть немного небрежен. Результат будет неотличим от случайной функции, хотя на самом деле таковой не является.
Результат будет неотличим от случайной функции, хотя на самом деле таковой не является. Вот почему современная теоретико-сложная криптография предполагает, что наши злоумышленники должны работать в течение некоторого разумного периода времени — обычно это количество временных шагов, полиномиальное по параметру безопасности схемы. Однако даже противник с ограниченным полиномиальным временем может попытаться подобрать сигнатуру методом грубой силы. Ее вероятность успеха может быть относительно небольшой, но она отлична от нуля: например, она может добиться успеха после первого предположения. Таким образом, на практике в определениях безопасности, таких как UF-CMA, мы требуем не «ни один злоумышленник никогда не сможет подделать подпись», а скорее «все злоумышленники преуспеют с минимальной вероятностью [в параметре безопасности схемы]», где пренебрежимо мала имеет очень конкретное значение.
Вот почему современная теоретико-сложная криптография предполагает, что наши злоумышленники должны работать в течение некоторого разумного периода времени — обычно это количество временных шагов, полиномиальное по параметру безопасности схемы. Однако даже противник с ограниченным полиномиальным временем может попытаться подобрать сигнатуру методом грубой силы. Ее вероятность успеха может быть относительно небольшой, но она отлична от нуля: например, она может добиться успеха после первого предположения. Таким образом, на практике в определениях безопасности, таких как UF-CMA, мы требуем не «ни один злоумышленник никогда не сможет подделать подпись», а скорее «все злоумышленники преуспеют с минимальной вероятностью [в параметре безопасности схемы]», где пренебрежимо мала имеет очень конкретное значение.
 Мы фокусируемся на веб-куки в HTTPS, поскольку это прекрасно иллюстрирует слабые стороны RC4 и силу нашей атаки.
Мы фокусируемся на веб-куки в HTTPS, поскольку это прекрасно иллюстрирует слабые стороны RC4 и силу нашей атаки. Документ
Вопросы и ответы
Чем эта атака отличается от предыдущих атак?
 Нам нужно всего 9⋅2 27 запросов и может заставить жертву генерировать 4450 запросов в секунду.
Это означает, что наша атака занимает всего 75 часов.
Мы также протестировали атаку на реальных устройствах, в то время как в предыдущих работах выполнялось только моделирование.
Нам нужно всего 9⋅2 27 запросов и может заставить жертву генерировать 4450 запросов в секунду.
Это означает, что наша атака занимает всего 75 часов.
Мы также протестировали атаку на реальных устройствах, в то время как в предыдущих работах выполнялось только моделирование. По их оценкам, для выполнения атаки требуется от 312 до 776 часов.
По их оценкам, для выполнения атаки требуется от 312 до 776 часов. Какие недостатки в RC4 используются для атаки?

Что теперь?
WPA-TKIP также уязвим?
 В общем, любой протокол, использующий RC4, следует считать уязвимым.
В общем, любой протокол, использующий RC4, следует считать уязвимым. Ресурсы
 Формат этих файлов и код для их простого чтения можно найти в этом файле Python.
Формат этих файлов и код для их простого чтения можно найти в этом файле Python. Служба управления ключами Amazon | Управление ключами шифрования
Уровень бесплатного пользования
Хранилище ключей
 созданный службой, пользовательским хранилищем ключей или импортированным вами. Для CMK с ключевым материалом, созданным службой, если вы согласились на автоматическую смену ключа каждый год, каждая новая версия ключа увеличивает стоимость CMK на 6,88 иен в месяц. Amazon KMS сохраняет и управляет каждой предыдущей версией CMK, чтобы убедиться, что вы можете расшифровать данные, зашифрованные в предыдущих версиях. За пары ключей данных, которые создаются запросами API GenerateDataKeyPair и GenerateDataKeyPairWithoutPlaintext, взимается плата за эти запросы API в соответствии с расценками на использование, описанными ниже. С вас не взимается ежемесячная плата за сами пары ключей данных, поскольку они не хранятся и не управляются службой. В месяц создания ключа ежемесячная плата за хранение ключа в размере 6,88 йены будет пропорциональна ближайшему полному часу.
созданный службой, пользовательским хранилищем ключей или импортированным вами. Для CMK с ключевым материалом, созданным службой, если вы согласились на автоматическую смену ключа каждый год, каждая новая версия ключа увеличивает стоимость CMK на 6,88 иен в месяц. Amazon KMS сохраняет и управляет каждой предыдущей версией CMK, чтобы убедиться, что вы можете расшифровать данные, зашифрованные в предыдущих версиях. За пары ключей данных, которые создаются запросами API GenerateDataKeyPair и GenerateDataKeyPairWithoutPlaintext, взимается плата за эти запросы API в соответствии с расценками на использование, описанными ниже. С вас не взимается ежемесячная плата за сами пары ключей данных, поскольку они не хранятся и не управляются службой. В месяц создания ключа ежемесячная плата за хранение ключа в размере 6,88 йены будет пропорциональна ближайшему полному часу. Вы не можете ни управлять жизненным циклом, ни правами доступа к управляемым ключам Amazon Web Services.
Вы не можете ни управлять жизненным циклом, ни правами доступа к управляемым ключам Amazon Web Services.
Использование ключа
Примеры цен
Пример Amazon EBS

Стоимость в месяц: 6,88 иен 1 СМК 0,15 йен (0,2 йены за 10 000 вызовов API) * 7500 вызовов Итого: 7,03 иен /месяц Amazon S3 Пример
Стоимость в месяц: 6,88 иен 1 СМК 40,2 йен Всего 2 010 000 запросов * 0,2 йены / 10 000 запросов Итого: 47,08 йен /месяц Пример приложения для подписи файлов

Стоимость в месяц: 6,88 иен 1 СМК 10,0 иен 100 000 запросов по 1,0 иены за 10 000 асимметричных запросов Итого: 16,88 иен /месяц 


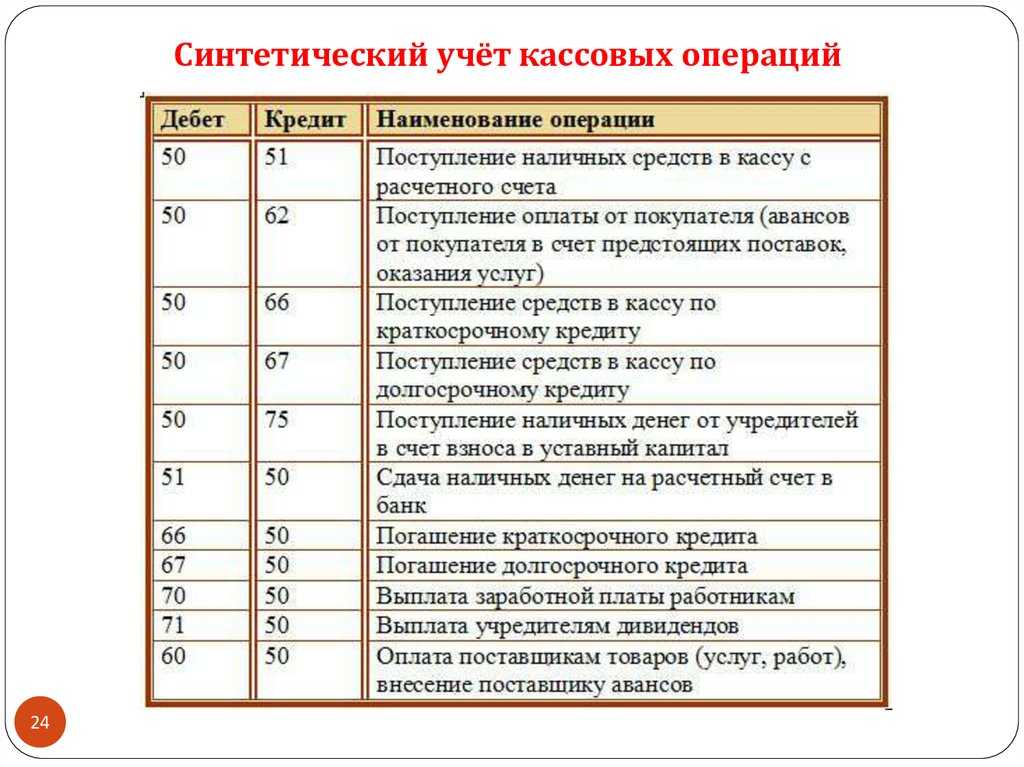 Т.е. вы видите и оцениваете текущую ситуацию на складе и можете быстро выявлять факторы повышенного риска, например, кража, повреждение товара и т.п. Вы можете быстрее оценивать продуктивность работы вашего персонала, и знать точно о времени выполнения той или иной операции, и, как следствие, какие процессы складской логистики у вас «проседают» и требуют доработок.
Т.е. вы видите и оцениваете текущую ситуацию на складе и можете быстро выявлять факторы повышенного риска, например, кража, повреждение товара и т.п. Вы можете быстрее оценивать продуктивность работы вашего персонала, и знать точно о времени выполнения той или иной операции, и, как следствие, какие процессы складской логистики у вас «проседают» и требуют доработок. 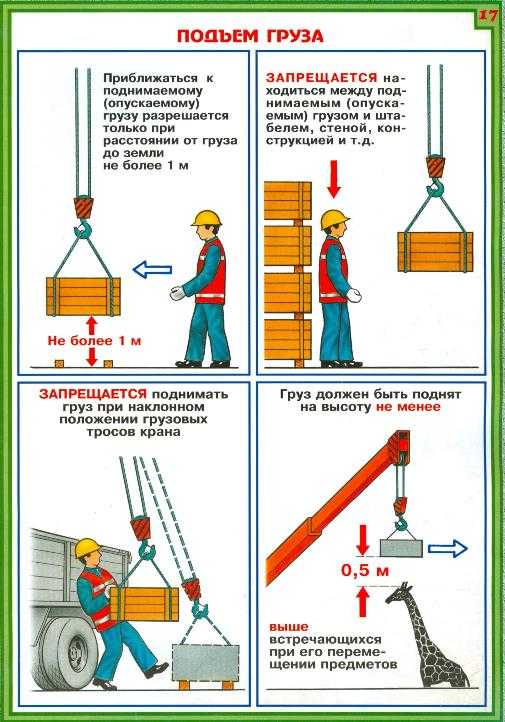
 Такая организация работы склада не только позволяет значительно сократить ошибки, но и повысить степень удовлетворенности ваших заказчиков, снизить количество отрицательных отзывов.
Такая организация работы склада не только позволяет значительно сократить ошибки, но и повысить степень удовлетворенности ваших заказчиков, снизить количество отрицательных отзывов.