Сотни тысяч маршрутов в секунду на ядро. Опыт Яндекс.Маршрутизации / Хабр
Пару недель назад Даня Тарарухин рассказал на Хабре, как появился наш сервис, Яндекс.Маршрутизация, и как он помогает компаниям с логистикой. Создавая платформу, мы решили несколько интересных проблем, одной из которых и посвящён сегодняшний пост. Я хочу поговорить о самом планировании маршрутов и необходимых для этого ресурсах.
Поиск оптимального маршрута между множеством точек — классическая задача дискретной оптимизации. Для её решения нужно знать расстояния и времена в пути между всеми точками. То есть — знать матрицу расстояний и времён. Ещё два года назад долгое вычисление матрицы было для нас очень критичной проблемой и блокировало развитие. Сам поиск оптимального решения при известной матрице занимал 10 минут, а вот вычисление всех ячеек матрицы для больших задач (на несколько тысяч заказов) занимало часы.
Чтобы решить задачу с пятью тысячами заказов, нужно знать расстояния и времена в пути между всеми точками. Это две матрицы чисел размерностью 5000х5000. Мы планируем маршруты курьеров на весь день, и утром курьер доедет от точки до точки за одно время, а вечером — за другое. Значит, нужно вычислять матрицы времён и расстояний для каждого часа дня. Не все часы дня уникальны, но пробочное время (утро и вечер) нужно покрыть хорошо. Поэтому мы пришли к конфигурации с тринадцатью часовыми срезами. Итого нам нужно два куба (времён и расстояний) размерностью 13х5000х5000 каждый. Это 325 млн маршрутов, посчитанных по реальному графу дорог, в котором 165 млн ребёр. Расчёт одного маршрута в хорошо оптимизированном алгоритме команды Яндекс.Карт занимает порядка 10 мс, суммарно получаем 900 часов вычислений. Даже при распараллеливании на 900 CPU нужно ждать 1 час. Такой сервис мы не могли запустить, нужен был более подходящий алгоритм.
Это две матрицы чисел размерностью 5000х5000. Мы планируем маршруты курьеров на весь день, и утром курьер доедет от точки до точки за одно время, а вечером — за другое. Значит, нужно вычислять матрицы времён и расстояний для каждого часа дня. Не все часы дня уникальны, но пробочное время (утро и вечер) нужно покрыть хорошо. Поэтому мы пришли к конфигурации с тринадцатью часовыми срезами. Итого нам нужно два куба (времён и расстояний) размерностью 13х5000х5000 каждый. Это 325 млн маршрутов, посчитанных по реальному графу дорог, в котором 165 млн ребёр. Расчёт одного маршрута в хорошо оптимизированном алгоритме команды Яндекс.Карт занимает порядка 10 мс, суммарно получаем 900 часов вычислений. Даже при распараллеливании на 900 CPU нужно ждать 1 час. Такой сервис мы не могли запустить, нужен был более подходящий алгоритм.
Для дальнейшего чтения полезно знать алгоритм Дейкстры для поиска кратчайшего пути в графе. Его можно представить как «волну», исходящую из точки старта маршрута и идущую кругом по всему графу до тех пор, пока не встретится точка финиша.
Почти каждый кандидат в разработчики на собеседовании догадывается до первого шага оптимизации такой задачи: можно запускать волну с двух сторон и заканчивать поиск, когда волны встретятся. Суммарная площадь двух волн половинного радиуса меньше одной большой.
Реальный граф дорог достаточно сильно структурирован, и это можно использовать. Когда вы ищете кратчайшее расстояние между Москвой и Питером, в классической Дейкстре вы будете вынуждены распространять волну по кругу и перебирать все улицы и переулки Москвы, подмосковных городов и деревень, улицы Твери и Новгорода. Это огромный объём вычислений, но можно заранее подготовиться и запомнить оптимальные маршруты между городами (aka шорткаты) и не повторять их в рантайме. Тогда для поиска маршрута между двумя точками в иерархической Дейкстре вам останется посчитать кратчайшие расстояния до нужного шортката.
Команда роутера Карт уже достаточно давно реализовала такие оптимизации. Именно они позволили достичь 10 мс для поиска маршрута между двумя точками. 🙂 Так что пока мы не приблизились к решению нашей проблемы.
Раз режим поиска точка-точка уже предельно оптимизирован, мы можем оптимизировать расчёт ряда в матрице. Ряд — это расстояния от одной точки до всех остальных. Пока мы ищем расстояние до самой дальней точки, мы попутно вычисляем расстояния до более близких. Значит, вычисление ряда эквивалентно вычислению расстояния до самой дальней точки.
Смотрим на время вычисления ряда по такому алгоритму и вспоминаем, что последовательное вычисление 5000 маршрутов заняло бы порядка 5000 * 10 мс = 50 с:
На графике показано время вычисления строки в матрице расстояний размером 1*N для разных N (по реальным данным). Видно, что вычисление строки интересующего нас размера 1*5000 укладывается в 1,3 секунды. На график добавлена линия тренда, которая показывает, что время вычислений растет чуть медленнее, чем линейно по N, порядок N**0.74
На график добавлена линия тренда, которая показывает, что время вычислений растет чуть медленнее, чем линейно по N, порядок N**0.74
Уже неплохо! С таким алгоритмом мы можем посчитать наш куб за 13 * 5000 * 1,3 с = 84 500 с = почти 24 часа. Он легко параллелится по рядам, и при использовании 50 CPU расстояния вычисляются за полчаса. Порядок сложности алгоритма вычисления куба — O(N**1.74):
График оценочного времени вычисления 13 матриц размером N*N по рядам на 50 CPU (домножили предыдущий график на 13*N/50). По этому графику мы принимали решение, что если к нам придет клиент с 5000 заказов, то мы должны уложиться в полчаса со всеми тринадцатью часовыми срезами. А вот если заказов станет 10 000, то всё плохо: придётся добавлять железо или увеличивать время.
В таком виде два с половиной года назад мы запустили первую версию нашего API, решающего логистическую задачу. Клиенты достаточно часто жаловались на долгое время решения, и их легко понять: ты запустил задачу решаться, ждёшь 1 час, получаешь решение и понимаешь, что забыл поправить время смены у водителя, исправляешь и всё начинается сначала.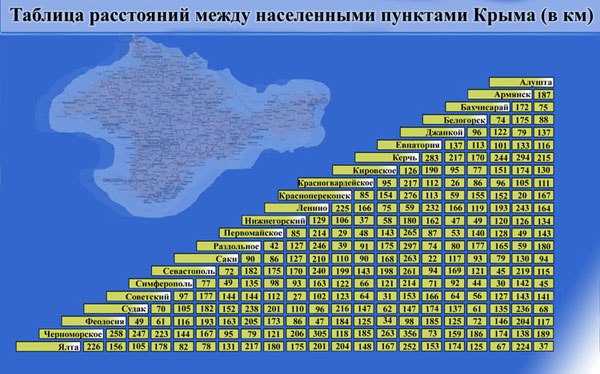 Водители начинают нервничать, так как рискуют попасть в утренний час пик, а то и вовсе не успеют доставить заказ в срок. Нужно было что-то делать. «Закидывать» проблему железом не хотелось: мы готовились к большим нагрузкам, потребовалось бы много железа, да и закупка серверов происходит не одномоментно.
Водители начинают нервничать, так как рискуют попасть в утренний час пик, а то и вовсе не успеют доставить заказ в срок. Нужно было что-то делать. «Закидывать» проблему железом не хотелось: мы готовились к большим нагрузкам, потребовалось бы много железа, да и закупка серверов происходит не одномоментно.
Изучение академических статей показало, что, оказывается, для этой задачи есть алгоритмы с линейной сложностью*! (В статье по ссылке есть большой обзор всевозможных современных способов ускорения Дейкстры, в том числе и для матричного случая.) Вычислять матрицу за линейное время — это не укладывалось в голове. Один из наших разработчиков вызвался написать прототип, и вот что получилось:
Время вычисления одной матрицы размера N*N на одном CPU с помощью алгоритма «быстрых матриц». Сложность получается порядка O(N**1,1). Высокие N выбиваются из линии тренда, поскольку на время уже больше влияет генерация ответа и его скачивание по сети.
115 секунд на матрицу 5000х5000 при использовании одного ядра и почти линейная зависимость от N. Фантастика стала реальностью! Идея алгоритма комбинирует две описанные выше идеи: Дейкстру для рядов и иерархический поиск. Очевидно, что, начав вычислять второй ряд, мы в какой-то момент вновь будем обходить ту же область графа, которую мы только что проходили, вычисляя предыдущий ряд. Поэтому давайте запоминать в узлах иерархического графа кратчайшие расстояния до всех destinations. Когда мы начнём вычислять следующий ряд, то, дойдя до такого узла, мы разом получим почти все расстояния до других точек.
Фантастика стала реальностью! Идея алгоритма комбинирует две описанные выше идеи: Дейкстру для рядов и иерархический поиск. Очевидно, что, начав вычислять второй ряд, мы в какой-то момент вновь будем обходить ту же область графа, которую мы только что проходили, вычисляя предыдущий ряд. Поэтому давайте запоминать в узлах иерархического графа кратчайшие расстояния до всех destinations. Когда мы начнём вычислять следующий ряд, то, дойдя до такого узла, мы разом получим почти все расстояния до других точек.
Полтора года назад это позволило нам сэкономить полчаса времени седения волос логиста и существенно уменьшить потребление железа. Если раньше на один большой запрос нам требовалось 50 ядер на полчаса, то теперь — 13 ядер на 2 минуты. Это примерно 200 000 маршрутов в секунду на ядро. Тот редкий случай, когда новый алгоритм не просто закрывает класс проблем, а расширяет наши представления о возможном.
* Статья «Route Planning in Transportation Networks», см. параграф 2.7.2 «Batched Shortest Paths»
параграф 2.7.2 «Batched Shortest Paths»
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Настройка карты — Яндекс Карты. Помощь
- Переместить карту
- Изменить тип карты
- Повернуть или наклонить карту
- Изменить масштаб карты
- Измерить расстояние
- Измерить площадь
- Распечатать карту по умолчанию карта вашего города или области.
Чтобы просмотреть другую область, щелкните левой кнопкой мыши и перетащите карту в нужном направлении.
В правом верхнем углу страницы нажмите и выберите режим отображения:
Выберите Карта для просмотра дорог, зданий и других объектов карты.
Выберите «Спутник», чтобы просмотреть фотографии местности, сделанные из космоса.
Выберите Гибрид для просмотра спутниковых изображений с дополнительными сведениями о карте (названия улиц, адреса и другая связанная информация).

Режим отображения не влияет на другие функции карты, такие как поиск, планирование маршрута или перетаскивание карты.
Вы можете вращать и наклонять карту только в режиме карты.
Внимание. Эта функция не поддерживается на устаревших и маломощных устройствах.
Для управления наклоном и вращением карты можно использовать:
Чтобы вернуть карту в исходное положение, один раз щелкните внешнее кольцо компаса.
При небольшом масштабе наклон сбрасывается автоматически.
Чтобы изменить масштаб карты, вы можете использовать:
Кнопки и .
Колесико мыши: прокручивайте назад для уменьшения и вперед для увеличения.
Кнопки мыши: увеличить карту двойным щелчком левой кнопкой мыши, уменьшить двойным щелчком правой кнопкой мыши.
Правая кнопка мыши:
Нажмите на карту.
Не отпуская кнопку, переместите мышь туда, куда вам нужно.

Перемещая мышь, вы выделяете область на карте.
Отпустите кнопку.
Выделенная область сместится в центр карты, и карта увеличится.
Вы можете измерять расстояние на карте по прямым и кривым линиям (например, чтобы проследить улицу).
Для этого выполните следующие действия:
В правом верхнем углу страницы щелкните . Убедитесь, что слева выбран параметр Измерить расстояние.
Чтобы отключить эту функцию, нажмите эту кнопку еще раз.
Выберите начальную точку измерения.
Выберите следующие точки. Длина всей линии будет отображаться рядом с последней точкой.
Вы можете настроить результирующую линию. Для этого щелкните любую точку и перетащите ее в другое место.
Если щелкнуть в любом месте линии, появится новая точка. Вы также можете перетаскивать его по карте.
Щелкните в любой точке.
 Вы увидите расстояние от начальной точки до выбранной точки, отображаемой рядом с ней.
Вы увидите расстояние от начальной точки до выбранной точки, отображаемой рядом с ней.Чтобы удалить точку, дважды щелкните по ней.
Чтобы удалить всю линию, щелкните рядом с конечной точкой.
Чтобы отключить линейку и удалить всю линию, щелкните рядом с конечной точкой.
Вы можете измерить площадь произвольного многоугольника.
Для этого выполните следующие действия:
В правом верхнем углу страницы щелкните . Выберите Планиметр слева.
Выберите начальную точку измерения на карте.
Выберите следующие точки для формирования многоугольника.
Полученный полигон можно настроить. Для этого щелкните любую точку и перетащите ее в другое место.
Если щелкнуть в любом месте линии, появится новая точка. Вы также можете перетаскивать его по карте.
Чтобы удалить точку, дважды щелкните по ней.
Вы можете перетащить полигон в другое место на карте.

Чтобы удалить весь многоугольник, щелкните рядом с конечной точкой.
Чтобы удалить полигон и выключить планиметр, щелкните рядом с конечной точкой.
Щелкните , затем выберите Печать. Откроется окно предварительного просмотра.
Увеличивайте и уменьшайте карту и перетаскивайте ее, если нужно.
Выберите:
Формат страницы:
Ориентация страницы:
Напишите комментарий, если вам нужно. Вы увидите комментарий, напечатанный под картой.
Щелкните Печать.
Выберите принтер и параметры печати.
Щелкните Печать.
Вы также можете распечатать собственную карту с нанесенными на нее элементами. Дополнительную информацию см. в Конструкторе карт.
Связаться со службой поддержки
Проложить маршрут — Мобильные Яндекс.Карты. Справка
Выбрав маршрут, нажмите «Начать!».

Приложение начнет отслеживать вас по мере движения по маршруту, используя информацию о вашем местоположении и ваши настройки. Вы можете:
Выбрать типы событий (например, предстоящие маневры), о которых вы хотите получать голосовые сообщения.;
Выберите язык голосовых сообщений (например, для предстоящих маневров).;
Выберите типы камер контроля скорости и дорожных событий, о которых вы хотите получать уведомления.
Установите, насколько допустимо превышение ограничения скорости, и приложение сообщит вам, когда вам нужно снизить скорость.
Выберите автоматическое масштабирование карты маршрута.
Примечание.
Дополнительные сведения об этих и других параметрах интерфейса приложения см. на странице settings_2.html#marsrut.
Когда вы в движении, приложение:
Сообщает вам о предстоящих поворотах и полосе движения:
Показывает вашу скорость, время и расстояние до конца маршрута .

Показывает заторы на дорогах, отображаемые цветами от зеленого до темно-красного вдоль вашего маршрута.
Уведомляет вас на экране и вслух.
Позволяет узнать, когда есть более быстрый маршрут.
Находит места на вашем маршруте.
Изменяет начальную или конечную точку маршрута.
Во время движения по маршруту доступна кнопка Меню. Он открывает меню со следующими пунктами:
Пробки — Отображает или скрывает пробки.
Полный вид — переключает вид с текущего сегмента маршрута на весь маршрут. Чтобы вернуться к крупному просмотру текущего сегмента маршрута, коснитесь «Продолжить».
Со звуком — включает или отключает голосовую навигацию.
Мои места — открывает список Мои места.
Дорожные события — Добавляет дорожное событие.
Настройки — открывает ваши настройки.
Примечание.

Вы можете отслеживать свою поездку по маршруту, построенному в приложении (если оно установлено на вашем устройстве).
О поворотах, дорожных событиях и камерах контроля скорости.
Просто включите дорожные события.
Чтобы получать уведомления на экране, а также читать их вслух:
Коснитесь Меню .
В открывшемся меню нажмите Громко .
Приложение начнет сообщать вам информацию о поворотах, дорожных событиях и камерах контроля скорости. Дополнительные сведения см. в описании параметра settings_2.html#marsrut__voice.
Чтобы отключить голосовые подсказки во время поездки, повторите действия 1 и 2.
Приложение может заметить, что есть более быстрый маршрут, пока вы едете. Это скажет вам сразу.
Нажмите на сообщение, чтобы переключиться на новый маршрут.
Чтобы быстро найти достопримечательности на маршруте:
Нажмите «Поиск» .
Вы увидите наиболее полезные для водителей категории.
 Выберите подходящий.
Выберите подходящий.Или коснитесь значка микрофона и скажите, что вы ищете.
Или коснитесь …больше и введите поисковый запрос в появившемся поле.
Найденные места будут отображаться на карте как .
Коснитесь одного из вариантов. Откроется панель с указанием расстояния до выбранного места и времени его работы.
Нажмите «Маршрут» и выберите один из следующих вариантов:
Через, чтобы сделать выбранную точку частью вашего маршрута.
Чтобы проложить маршрут к выбранной точке.
Чтобы отменить выбор, нажмите где-нибудь на карте за пределами панели.
Примечание.
Вы также можете выбрать точку на карте. См. также Изменение начальной или конечной точки маршрута.
Если после создания маршрута вы хотите изменить начальную или конечную точку вашего маршрута:
Нажмите и удерживайте соответствующую точку на карте, после чего откроется контекстное меню.



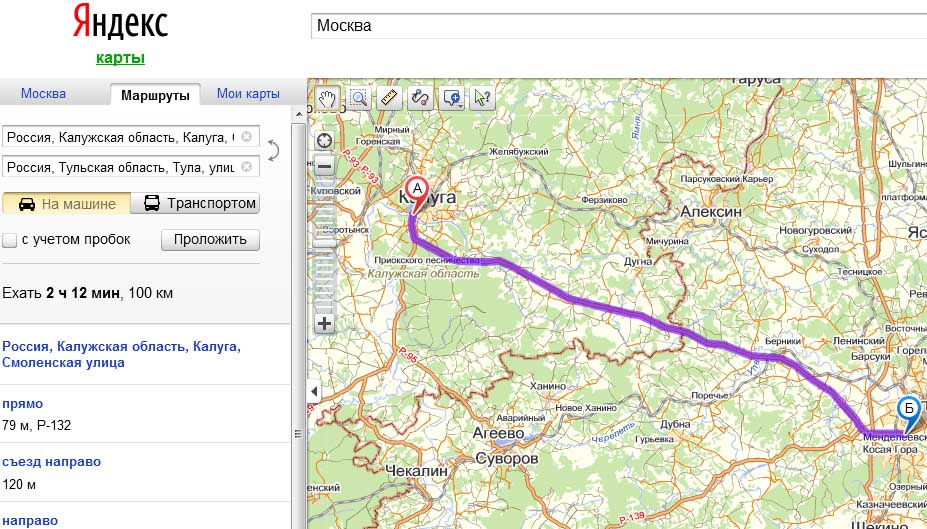
 Сравните красную линию, по которой Яндекс измерил расстояние, и зелёный отрезок прямой, который я сам нарисовал.
Сравните красную линию, по которой Яндекс измерил расстояние, и зелёный отрезок прямой, который я сам нарисовал. На схеме ортодромия показана тёмно-зелёной линией
На схеме ортодромия показана тёмно-зелёной линией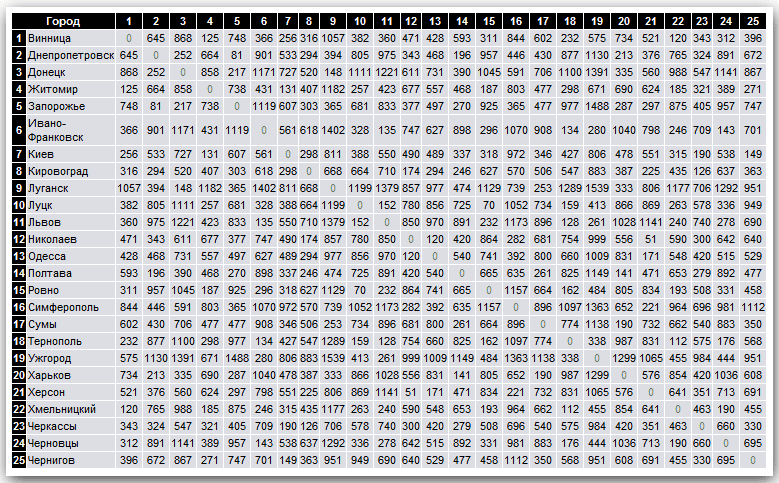 Но ортодромия пересекает меридианы под разными углами. А линия, пересекающая параллельные прямые под разными углами, прямой быть ну никак не может. Она будет как раз-таки кривой.
Но ортодромия пересекает меридианы под разными углами. А линия, пересекающая параллельные прямые под разными углами, прямой быть ну никак не может. Она будет как раз-таки кривой. Ведь меридианы тоже являются дугами большого круга, это очевидно из рисунка (3). Эксперимент с меридианами, если хотите, проведите сами.
Ведь меридианы тоже являются дугами большого круга, это очевидно из рисунка (3). Эксперимент с меридианами, если хотите, проведите сами. Главное, чтобы они были как можно дальше друг от друга. Для наглядности — не менее тысячи километров.
Главное, чтобы они были как можно дальше друг от друга. Для наглядности — не менее тысячи километров. Кривая линейка Яндекс.Кар
Кривая линейка Яндекс.Кар
 Блин. Затупил немного — нет, все локсодромии прямые только на Меркаторе. Всё. То есть должны быть и цилиндричность, и равноугольность. Wiki it!
Блин. Затупил немного — нет, все локсодромии прямые только на Меркаторе. Всё. То есть должны быть и цилиндричность, и равноугольность. Wiki it!
 Просто глобус, который можно приближать-удалять. Там, я так понимаю, вообще искажений нет. Это ж глобус.
Просто глобус, который можно приближать-удалять. Там, я так понимаю, вообще искажений нет. Это ж глобус. 48184250%2C5.20218746~130.07797405%2C23.02019655
48184250%2C5.20218746~130.07797405%2C23.02019655 (В смысле точек бесконечно много поставить)
(В смысле точек бесконечно много поставить)

 Вы увидите расстояние от начальной точки до выбранной точки, отображаемой рядом с ней.
Вы увидите расстояние от начальной точки до выбранной точки, отображаемой рядом с ней.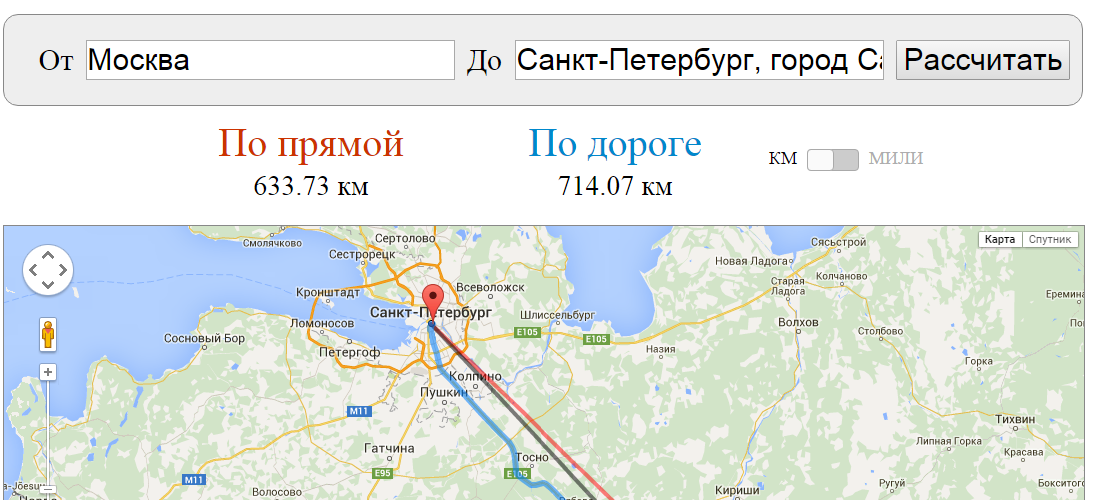


 Выберите подходящий.
Выберите подходящий.